1. 估算一下圆的面积大约是( )个小方格。
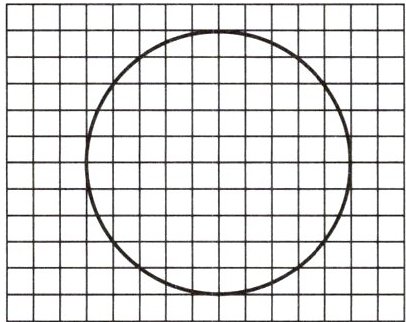

答案:
42
2. 如图,把一个圆分成若干(偶数)等份后,拼成了一个近似的平行四边形,这个平行四边形的底近似于圆的周长的( ),高近似于圆的( )。因为平行四边形的面积= ( )×( ),所以圆的面积 $ S = $ ( )。(用字母表示)
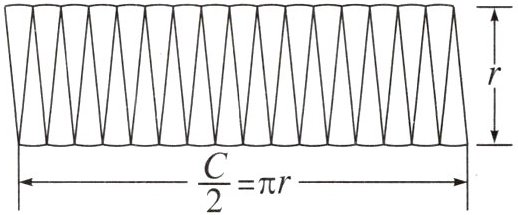

答案:
$\frac{1}{2}$,半径,底,高,$\pi r^2$
3. 大圆的直径是小圆直径的4倍。大圆的周长是小圆周长的( )倍,大圆的面积是小圆面积的( )倍。
答案:
4,16
1. 求某自动旋转喷灌装置喷水的范围,就是求圆的( )。
A.周长
B.面积
C.圆周率
D.半径
A.周长
B.面积
C.圆周率
D.半径
答案:
B
2. 一个圆的半径是 $ 3 \, cm $,另一个圆的直径是 $ 4 \, cm $,则这两个圆的面积相差( ) $ cm^2 $。
A.$ 3.14 $
B.$ 15.7 $
C.$ 21.98 $
D.$ 62.8 $
A.$ 3.14 $
B.$ 15.7 $
C.$ 21.98 $
D.$ 62.8 $
答案:
B
3. 若大圆的半径是 $ r $,小圆的直径是 $ r $,则小圆的面积是大圆面积的( )。
A.$ \dfrac{1}{2} $
B.$ \dfrac{1}{4} $
C.$ \dfrac{1}{8} $
D.$ \dfrac{1}{16} $
A.$ \dfrac{1}{2} $
B.$ \dfrac{1}{4} $
C.$ \dfrac{1}{8} $
D.$ \dfrac{1}{16} $
答案:
B
三、求下列各圆的面积。(单位:$ cm $)
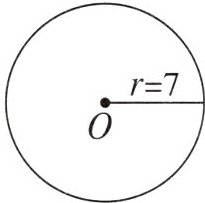
1.
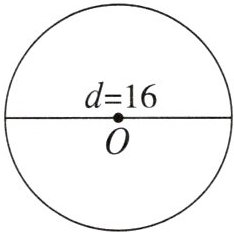
2.
1.

2.

答案:
1.
解:$S = \pi r^2$,
$S = 3.14 × 7^2$,
$S = 3.14 × 49$,
$S = 153.86 cm^2$。
答:面积为$153.86 cm^2$。
2.
解:$r = \frac{d}{2} = \frac{16}{2} = 8 $,
$S = \pi r^2$,
$S = 3.14 × 8^2$,
$S = 3.14 × 64$,
$S = 200.96 cm^2$。
答:面积为$200.96 cm^2$。
解:$S = \pi r^2$,
$S = 3.14 × 7^2$,
$S = 3.14 × 49$,
$S = 153.86 cm^2$。
答:面积为$153.86 cm^2$。
2.
解:$r = \frac{d}{2} = \frac{16}{2} = 8 $,
$S = \pi r^2$,
$S = 3.14 × 8^2$,
$S = 3.14 × 64$,
$S = 200.96 cm^2$。
答:面积为$200.96 cm^2$。
四、解决问题。
如图,将一个圆剪拼成一个近似的长方形,已知长方形的周长是 $ 33.12 \, dm $,求圆的面积。
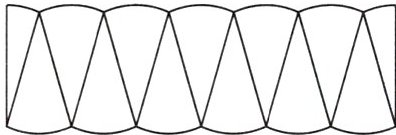
如图,将一个圆剪拼成一个近似的长方形,已知长方形的周长是 $ 33.12 \, dm $,求圆的面积。

答案:
设圆的半径为$ r \, dm $。
1. 拼成的近似长方形的长为圆周长的一半,即$ \pi r \, dm $,宽为圆的半径$ r \, dm $。
2. 长方形周长公式:$ 2×(长 + 宽) = 33.12 \, dm $,代入得:$ 2×(\pi r + r) = 33.12 $。
3. 化简:$ 2r(\pi + 1) = 33.12 $,取$ \pi = 3.14 $,则$ 2r(3.14 + 1) = 8.28r = 33.12 $。
4. 解得半径:$ r = 33.12 ÷ 8.28 = 4 \, dm $。
5. 圆的面积:$ S = \pi r^2 = 3.14 × 4^2 = 50.24 \, dm^2 $。
答:圆的面积是$ 50.24 \, dm^2 $。
1. 拼成的近似长方形的长为圆周长的一半,即$ \pi r \, dm $,宽为圆的半径$ r \, dm $。
2. 长方形周长公式:$ 2×(长 + 宽) = 33.12 \, dm $,代入得:$ 2×(\pi r + r) = 33.12 $。
3. 化简:$ 2r(\pi + 1) = 33.12 $,取$ \pi = 3.14 $,则$ 2r(3.14 + 1) = 8.28r = 33.12 $。
4. 解得半径:$ r = 33.12 ÷ 8.28 = 4 \, dm $。
5. 圆的面积:$ S = \pi r^2 = 3.14 × 4^2 = 50.24 \, dm^2 $。
答:圆的面积是$ 50.24 \, dm^2 $。
五、奇思妙想。
如图,一块边长为 $ 10 \, m $ 的正方形草地,在相对的一对顶点上各有一棵树,树上各拴着一头牛,绳长都是 $ 10 \, m $,两头牛都能吃到的草地面积是多少平方米?
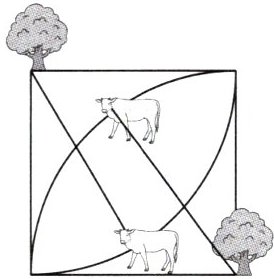
如图,一块边长为 $ 10 \, m $ 的正方形草地,在相对的一对顶点上各有一棵树,树上各拴着一头牛,绳长都是 $ 10 \, m $,两头牛都能吃到的草地面积是多少平方米?

答案:
57平方米。
查看更多完整答案,请扫码查看


