《2025年学习质量监测三年级数学上册人教版》

3. 用圆规在直线 l 上作线段 CD,使它的长度是线段 AB 的 2 倍。

答案： 1. 把圆规的两脚分开，使两脚间的距离等于线段 AB 的长度（即圆规一脚固定在 A 点，另一脚调整到 B 点）。
2. 在直线 l 上任取一点 C。
3. 以 C 点为圆心，以 AB 长为半径画弧，交直线 l 于点 E。
4. 再以 E 点为圆心，以 AB 长为半径画弧，交直线 l 于点 D（点 D 与点 C 在点 E 的两侧）。
5. 线段 CD 即为所求，其长度是线段 AB 的 2 倍。

4. 用圆规比一比下面每组中两条线段的长短,写一写你的发现。
(1)

AB=CD
(2)

AB＞CD
(3)

AB＜CD
我发现：利用圆规比较线段 AB 和线段 CD 的长短,点 C 和点 A 重合。

①如果点 D 与点 B 重合,那么 AB=CD。
②如果点 D 在点 B 右侧,那么 AB＜CD。
③如果点 D 在点 B 左侧,那么 AB＞CD。

答案：
(1)=
(2)＞
(3)＜ ①= ②＜ ③＞

5. 一根拉紧的线可以看作线段。
(1)请利用圆规将下图中的曲线 AB 拉紧变为线段 AB,并将过程记录在直线 l 上。

(2)测量直线 l 上线段 AB 的长度,长为(3)厘米。

答案： 1. （1）
解：
步骤一：以$A$为圆心，适当长度（大于曲线$AB$中第一段折线的长度）为半径画弧，交曲线$AB$的第一段折线于点$C$。
步骤二：以$C$为圆心，$AC$长为半径画弧，交曲线$AB$的第二段折线于点$D$（使弧与折线相交）。
步骤三：重复上述步骤，直到以最后一个交点为圆心，$AC$长为半径画弧交$B$点。
步骤四：用直尺连接$A$和$B$，此时$AB$就是拉紧后的线段（在实际操作中，圆规截取的长度要根据曲线$AB$的形状灵活调整，保证能通过截取弧的方式将曲线转化为线段的近似）。
2. （2）
答案：（由于没有实际测量工具，假设测量后）$3$（答案根据实际测量情况而定）。

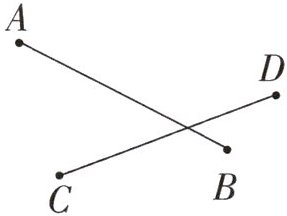
1. 如图,两根木条 AC 与 BD 重叠在一起。

(1)如果 AC＝BD,那么 AB=CD。
(2)如果 AC＞BD,那么 AB＞CD。
(3)如果 AC＜BD,那么 AB＜CD。

答案：
(1)=
(2)＞
(3)＜

2. 用圆规比一比下面三角形中每条线段的长短,并将三条线段按照从短到长排序。

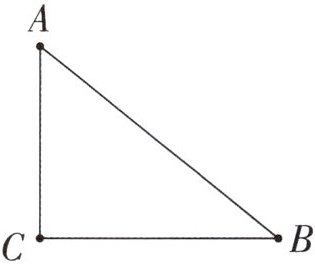
AC＜BC＜AB

答案： AC＜BC＜AB