1. 下面四个现象中,能用“两点间所有连线中线段最短”解释的是(
A.把一根木条固定在墙上至少需要 2 枚钉子
B.植树时,只要定出两棵树的位置,就能确定同一行树所在的位置
C.从 A 地到 B 地架设电线,总是尽可能沿着线段 AB 架设
D.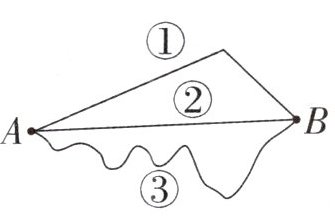
如图从 A 到 B 走路线②最近
D
)。A.把一根木条固定在墙上至少需要 2 枚钉子
B.植树时,只要定出两棵树的位置,就能确定同一行树所在的位置
C.从 A 地到 B 地架设电线,总是尽可能沿着线段 AB 架设
D.

如图从 A 到 B 走路线②最近
答案:
D
2. 如图,用圆规比较线段 AB 和 CD 的长度,下列选项正确的是(
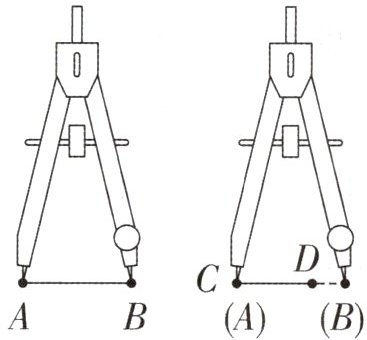
A.AB>CD
B.AB=CD
C.AB<CD
D.无法确定
A
)。
A.AB>CD
B.AB=CD
C.AB<CD
D.无法确定
答案:
A
3. 如图,如果 AB<CD,那么 AC 与 BD 的关系是(

A.AC>BD
B.AC=BD
C.AC<BD
D.无法确定
C
)。
A.AC>BD
B.AC=BD
C.AC<BD
D.无法确定
答案:
C
4. 如图,从 A 到 B 有三条路线可以选择,这三条路线长度的大小关系是(
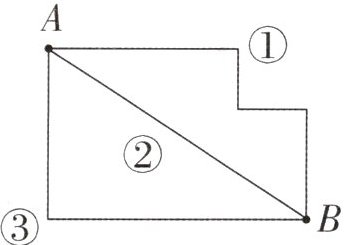
A.①>③>②
B.①=③>②
C.③>①>②
D.无法判断
B
)。
A.①>③>②
B.①=③>②
C.③>①>②
D.无法判断
答案:
B
1. 用圆规比较哪只蜗牛爬行的路线比较长(在图中呈现出比较过程)。

结论:(

结论:(
②
)号蜗牛爬行的路线比较长。
答案:
②
2. 在直线 l 上画出 2 厘米的线段 AB,再用圆规在直线 l 上作线段 CA,使 CA=AB。

1. 从直线 $l$ 上一点 $A$(可自行确定点 $A$位置)开始,用直尺沿直线 $l$ 量出 $2$ 厘米,标记出点 $B$,则线段 $AB$ 为所求作的 $2$ 厘米线段。
2. 把圆规两脚张开到 $AB$ 的长度($2$ 厘米),以点 $A$ 为圆心(一部分脚对准点 $A$),在直线 $l$ 上与 $B$ 相反方向截取,得到点 $C$,则线段 $CA$ 满足 $CA = AB$。

1. 从直线 $l$ 上一点 $A$(可自行确定点 $A$位置)开始,用直尺沿直线 $l$ 量出 $2$ 厘米,标记出点 $B$,则线段 $AB$ 为所求作的 $2$ 厘米线段。
2. 把圆规两脚张开到 $AB$ 的长度($2$ 厘米),以点 $A$ 为圆心(一部分脚对准点 $A$),在直线 $l$ 上与 $B$ 相反方向截取,得到点 $C$,则线段 $CA$ 满足 $CA = AB$。
答案:
1. 从直线 $l$ 上一点 $A$(可自行确定点 $A$位置)开始,用直尺沿直线 $l$ 量出 $2$ 厘米,标记出点 $B$,则线段 $AB$ 为所求作的 $2$ 厘米线段。
2. 把圆规两脚张开到 $AB$ 的长度($2$ 厘米),以点 $A$ 为圆心(一部分脚对准点 $A$),在直线 $l$ 上与 $B$ 相反方向截取,得到点 $C$,则线段 $CA$ 满足 $CA = AB$。
2. 把圆规两脚张开到 $AB$ 的长度($2$ 厘米),以点 $A$ 为圆心(一部分脚对准点 $A$),在直线 $l$ 上与 $B$ 相反方向截取,得到点 $C$,则线段 $CA$ 满足 $CA = AB$。
查看更多完整答案,请扫码查看


