第74页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
12. 在□里填合适的数。
5 + 5 = 2 +
10 - 2 = 4 +
5 + 5 = 2 +
8
3 + 4 = 6
+ 110 - 2 = 4 +
4
9 - 3 = 3 + 3
答案:
解析:
本题主要考查加减法运算以及等式的性质。
对于第一个等式 5 + 5 = 2 + □:
先计算左边的和:5 + 5 = 10,
再计算右边的已知部分:2,
想:哪个数与2相加等于10,即 10 - 2 = 8,
所以,第一个□里填 8。
对于第二个等式 3 + 4 = □ + 1:
先计算左边的和:3 + 4 = 7,
再计算右边的已知部分:1,
想:哪个数与1相加等于7,即 7 - 1 = 6,
所以,第二个□里填 6。
对于第三个等式 10 - 2 = 4 + □:
先计算左边的差:10 - 2 = 8,
再计算右边的已知部分:4,
想:哪个数与4相加等于8,即 8 - 4 = 4,
所以,第三个□里填 4。
对于第四个等式 9 - 3 = 3 + □:
先计算左边的差:9 - 3 = 6,
再计算右边的已知部分:3,
想:哪个数与3相加等于6,即 6 - 3 = 3,
所以,第四个□里填 3。
答案:
8;6;4;3。
本题主要考查加减法运算以及等式的性质。
对于第一个等式 5 + 5 = 2 + □:
先计算左边的和:5 + 5 = 10,
再计算右边的已知部分:2,
想:哪个数与2相加等于10,即 10 - 2 = 8,
所以,第一个□里填 8。
对于第二个等式 3 + 4 = □ + 1:
先计算左边的和:3 + 4 = 7,
再计算右边的已知部分:1,
想:哪个数与1相加等于7,即 7 - 1 = 6,
所以,第二个□里填 6。
对于第三个等式 10 - 2 = 4 + □:
先计算左边的差:10 - 2 = 8,
再计算右边的已知部分:4,
想:哪个数与4相加等于8,即 8 - 4 = 4,
所以,第三个□里填 4。
对于第四个等式 9 - 3 = 3 + □:
先计算左边的差:9 - 3 = 6,
再计算右边的已知部分:3,
想:哪个数与3相加等于6,即 6 - 3 = 3,
所以,第四个□里填 3。
答案:
8;6;4;3。
13. 已经铺了( )块,还要铺( )块才能铺满。

 在○里填数,使每条线上三个数连加都等于10。
在○里填数,使每条线上三个数连加都等于10。
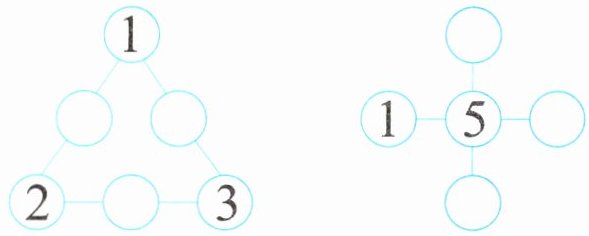
1
○ ○
○ ○
○
1 5 ○
○

 在○里填数,使每条线上三个数连加都等于10。
在○里填数,使每条线上三个数连加都等于10。
1
○ ○
○ ○
○
1 5 ○
○
答案:
对于第一组问题(已经铺了和还要铺的问题):
由于缺少具体的图形描述和铺砖的规则,无法直接给出已经铺了多少块和还需要铺多少块的答案。
假设图形是一个简单的矩形区域,部分区域已经铺满,但不知道具体数量和布局。
解析:此题考察的是对图形的观察和计数能力,以及对剩余数量的估算。
答案:无法直接给出答案,因为缺少具体图形信息。
对于第二组问题(在○里填数,使每条线上三个数连加都等于10):
这个问题是一个简单的算术问题,需要在○里填上数字,使得每条线上的三个数相加都等于10。
我们可以从给定的数字出发,尝试找到合适的数字填入○中。
假设图形是一个简单的线条连接问题,每条线上有三个位置需要填数,且每条线的和都应为10。
解析:此题考察的是基础的算术能力和逻辑推理能力。
给定数字中已经有1和5,因此每条线上还需要一个数字使得总和为10。
通过简单的减法,我们可以得出还需要的数字:10 - 1 - 5 = 4。
答案:
对于第一条线(从上到下):假设最上边的○为a,中间○为b,则:
1 + a + b = 10,考虑到其他线的条件,一个可能的答案是 a = 3, b = 6(答案不唯一,只要满足每条线总和为10即可)。
对于中间线(从左到右):假设左边○为c,右边○为d,则:
c + 5 + d = 10,考虑到已经使用的数字和每条线的总和,一个可能的答案是 c = 2, d = 3(注意避免重复和矛盾)。
对于最下边的线(从左到右,且只有一个空○):
假设这个○为e,则:1 + 5 + e = 10,解得 e = 4。
综合以上,一个可能的填充方案是(答案不唯一):
1
○3 ○6
○2 ○3
○
1 5 ○4
○
只要确保每条线上的数字相加等于10即可。
由于缺少具体的图形描述和铺砖的规则,无法直接给出已经铺了多少块和还需要铺多少块的答案。
假设图形是一个简单的矩形区域,部分区域已经铺满,但不知道具体数量和布局。
解析:此题考察的是对图形的观察和计数能力,以及对剩余数量的估算。
答案:无法直接给出答案,因为缺少具体图形信息。
对于第二组问题(在○里填数,使每条线上三个数连加都等于10):
这个问题是一个简单的算术问题,需要在○里填上数字,使得每条线上的三个数相加都等于10。
我们可以从给定的数字出发,尝试找到合适的数字填入○中。
假设图形是一个简单的线条连接问题,每条线上有三个位置需要填数,且每条线的和都应为10。
解析:此题考察的是基础的算术能力和逻辑推理能力。
给定数字中已经有1和5,因此每条线上还需要一个数字使得总和为10。
通过简单的减法,我们可以得出还需要的数字:10 - 1 - 5 = 4。
答案:
对于第一条线(从上到下):假设最上边的○为a,中间○为b,则:
1 + a + b = 10,考虑到其他线的条件,一个可能的答案是 a = 3, b = 6(答案不唯一,只要满足每条线总和为10即可)。
对于中间线(从左到右):假设左边○为c,右边○为d,则:
c + 5 + d = 10,考虑到已经使用的数字和每条线的总和,一个可能的答案是 c = 2, d = 3(注意避免重复和矛盾)。
对于最下边的线(从左到右,且只有一个空○):
假设这个○为e,则:1 + 5 + e = 10,解得 e = 4。
综合以上,一个可能的填充方案是(答案不唯一):
1
○3 ○6
○2 ○3
○
1 5 ○4
○
只要确保每条线上的数字相加等于10即可。
查看更多完整答案,请扫码查看


