1. 在实际使用中,人们常将
2. 滑轮组绳子的段数n是指连接在
3. 用滑轮组吊起重物,滑轮组用n段绳子吊重物,绳子自由端移动的距离s就是重物提升高度h的
4. 轮轴由具有共同转轴的大轮和小轮组成. 轮轴可以看成是杠杆的变形. 轴心O为支点,大轮半径R和小轮半径r分别为动力臂和阻力臂. 根据杠杆原理可得$F_1R=$
动
滑轮和定
滑轮组合成滑轮组,这样既可以省力
又可以改变施力的方向
。2. 滑轮组绳子的段数n是指连接在
动
滑轮上的绳子的段数,滑轮组绳子固定端在定滑轮的钩上,滑轮组绳子段数是偶
数;固定端在动滑轮的钩上,段数是奇
数,简称“奇动偶定”。3. 用滑轮组吊起重物,滑轮组用n段绳子吊重物,绳子自由端移动的距离s就是重物提升高度h的
n
倍,即s=n
h;在不计摩擦和绳重时,提起重物的力就是重物和动滑轮总重的$\frac{1}{n}$
,即F=$\frac{G_{总}}{n}$
=$\frac{G_{物}+G_{动}}{n}$
;若不考虑摩擦、绳重和动滑轮的自重,则F=$\frac{G_{物}}{n}$
。4. 轮轴由具有共同转轴的大轮和小轮组成. 轮轴可以看成是杠杆的变形. 轴心O为支点,大轮半径R和小轮半径r分别为动力臂和阻力臂. 根据杠杆原理可得$F_1R=$
$F_{2}r$
. 因为R>r,所以$F_1<F_2,$这种轮轴相当于一种省力
杠杆. 如门把手、汽车方向盘和扳手都是应用轮轴的实例.
答案:
1.动 定 省力 施力的方向 2.动 偶 奇 3.n n $\frac{1}{n}$ $\frac{G_{总}}{n}$ $\frac{G_{物}+G_{动}}{n}$ $\frac{G_{物}}{n}$ 4.$F_{2}r$ 省力
1. 如图所示,如果绳重和摩擦不计,动滑轮重不计,物重G= 300N,则图甲中的拉力Fₐ=
150
N,图乙中的拉力Fᵦ=100
N;如果不计绳重及摩擦,动滑轮的重力为30N,物重G= 300N,则拉力Fₐ=165
N,拉力Fᵦ=110
N. 若甲、乙两装置中绳子自由端均移动了1.2m,则甲装置中物体被提升的高度为0.6
m,乙装置中物体被提升的高度为0.4
m.
答案:
1.150 100 165 110 0.6 0.4
2. 根据图中各滑轮组的省力要求,画出各滑轮组上绳子的绕法. (不计动滑轮重和摩擦)
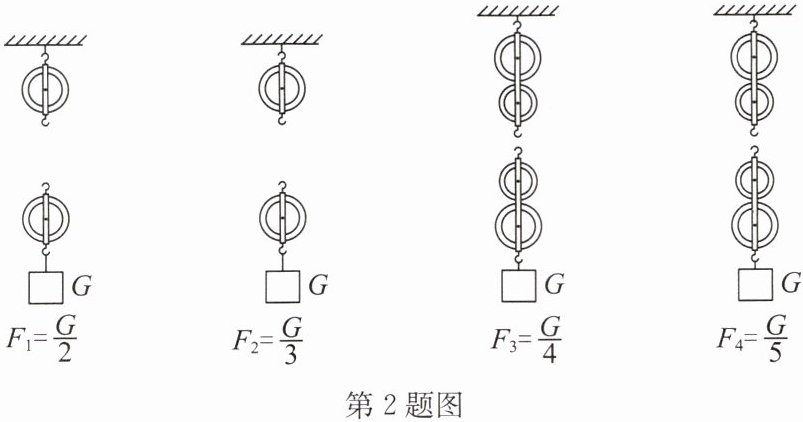

答案:
2.如答图所示

2.如答图所示

查看更多完整答案,请扫码查看


