1. 用长10米的铝合金条制成“目”字形的落地窗框(如图),问宽和高各为多长时,该窗户的透光面积为3平方米?(铝合金条的宽度不计、接口损耗不计)


答案:
解:设宽为 x 米,则高为$\frac {10-4x}{2}$米.
依题意得$x×\frac {10-4x}{2}=3$,
整理得$2x^{2}-5x+3=0$,
解得$x_{1}=1,x_{2}=\frac {3}{2}$.
当$x=1$时,$\frac {10-4x}{2}=3$;当$x=\frac {3}{2}$时,$\frac {10-4x}{2}=2$.
答:当宽为 1 米,高为 3 米时或当宽为$\frac {3}{2}$米,高为 2 米时,该窗户的透光面积为 3 平方米.
依题意得$x×\frac {10-4x}{2}=3$,
整理得$2x^{2}-5x+3=0$,
解得$x_{1}=1,x_{2}=\frac {3}{2}$.
当$x=1$时,$\frac {10-4x}{2}=3$;当$x=\frac {3}{2}$时,$\frac {10-4x}{2}=2$.
答:当宽为 1 米,高为 3 米时或当宽为$\frac {3}{2}$米,高为 2 米时,该窗户的透光面积为 3 平方米.
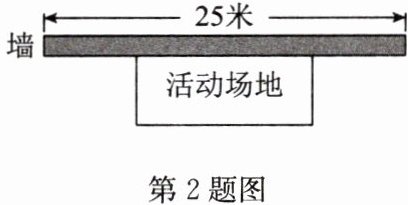
2. 如图,学校有一个面积为182平方米的长方形的活动场地,场地一边靠墙(墙长25米),另三面用长40米的合金栏网围成. 请你计算一下活动场地的长和宽.

答案:
解:设活动场地垂直于墙的一边长为 x 米,则另一边长为$(40-2x)$米.
依题意,得$x(40-2x)=182$,
整理,得$x^{2}-20x+91=0$,
解得$x_{1}=7,x_{2}=13$.
当$x=7$时,$40-2x=26>25$,不合题意,舍去.
当$x=13$时,$40-2x=14<25$,符合题意.
答:活动场地的长为 14 米,宽为 13 米.
依题意,得$x(40-2x)=182$,
整理,得$x^{2}-20x+91=0$,
解得$x_{1}=7,x_{2}=13$.
当$x=7$时,$40-2x=26>25$,不合题意,舍去.
当$x=13$时,$40-2x=14<25$,符合题意.
答:活动场地的长为 14 米,宽为 13 米.
3. 有一张面积为100 $ \text{cm}^2 $ 的正方形贺卡,另有一个长方形信封(如图),长、宽之比为5:3,面积为150 $ \text{cm}^2 $,能将这张贺卡不折叠地放入此信封吗?请通过计算说明你的判断.

答案:
解:设长方形信封的长为 5x cm,则宽为 3x cm.
根据题意,得$5x\cdot 3x=150$,
解得$x_{1}=\sqrt {10},x_{2}=-\sqrt {10}$(不合题意,舍去).
∴长方形信封的宽为$3\sqrt {10}cm$.
$\because \sqrt {100}=10$,
∴正方形贺卡的边长为 10 cm.
$\because (3\sqrt {10})^{2}=90$,而$90<100,\therefore 3\sqrt {10}<10$.
答:不能将这张贺卡不折叠地放入此信封中.
根据题意,得$5x\cdot 3x=150$,
解得$x_{1}=\sqrt {10},x_{2}=-\sqrt {10}$(不合题意,舍去).
∴长方形信封的宽为$3\sqrt {10}cm$.
$\because \sqrt {100}=10$,
∴正方形贺卡的边长为 10 cm.
$\because (3\sqrt {10})^{2}=90$,而$90<100,\therefore 3\sqrt {10}<10$.
答:不能将这张贺卡不折叠地放入此信封中.
4. 如图,用一条长40 m的绳子围成矩形ABCD,设边AB的长为x m.
(1)边BC的长为
(2)矩形ABCD的面积是否可以是120 $ \text{m}^2 $?请给出你的结论,并用所学的方程知识说明理由.
解:不可以.理由:若矩形 ABCD 的面积是$120m^{2}$,根据题意,得$-x^{2}+20x=120$,即$x^{2}-20x+120=0$.
$\because b^{2}-4ac=-80<0$,∴这个方程无实数根.
∴矩形 ABCD 的面积不可以是$120m^{2}$.
(1)边BC的长为
20-x
m,矩形ABCD的面积为-x²+20x
$ \text{m}^2 $;(均用含x的代数式表示)(2)矩形ABCD的面积是否可以是120 $ \text{m}^2 $?请给出你的结论,并用所学的方程知识说明理由.
解:不可以.理由:若矩形 ABCD 的面积是$120m^{2}$,根据题意,得$-x^{2}+20x=120$,即$x^{2}-20x+120=0$.
$\because b^{2}-4ac=-80<0$,∴这个方程无实数根.
∴矩形 ABCD 的面积不可以是$120m^{2}$.
答案:
(1)$20-x$$-x^{2}+20x$
(2)解:不可以.理由:若矩形 ABCD 的面积是$120m^{2}$,根据题意,得$-x^{2}+20x=120$,即$x^{2}-20x+120=0$.
$\because b^{2}-4ac=-80<0$,
∴这个方程无实数根.
∴矩形 ABCD 的面积不可以是$120m^{2}$.
(1)$20-x$$-x^{2}+20x$
(2)解:不可以.理由:若矩形 ABCD 的面积是$120m^{2}$,根据题意,得$-x^{2}+20x=120$,即$x^{2}-20x+120=0$.
$\because b^{2}-4ac=-80<0$,
∴这个方程无实数根.
∴矩形 ABCD 的面积不可以是$120m^{2}$.
查看更多完整答案,请扫码查看


