《2025年通城学典暑期升级训练八年级物理苏科版延边大学出版社》

19. (8分)如图所示是一种新型破窗锤,外观精致,既能破窗,又能割断安全带,深受广大车友欢迎。

(1)已知破窗锤的质量为 $ 150 \, \text{g} $,求破窗锤的重力。($ g $ 取 $ 10 \, \text{N/kg} $)
(2)若敲击处玻璃能承受的最大压强为 $ 1.5 × 10^7 \, \text{Pa} $,锤尖的面积为 $ 2 \, \text{mm}^2 $,则至少要用多大的压力才能敲碎玻璃？

答案： （1）已知破窗锤的质量$m=150\ \text{g}=0.15\ \text{kg}$,则破窗锤的重力$G=mg=0.15\ \text{kg}×10\ \text{N/kg}=1.5\ \text{N}$ （2）已知敲击处玻璃能承受的最大压强$p=1.5×10^{7}\ \text{Pa}$,锤尖的面积$S=2\ \text{mm}^{2}=2×10^{-6}\ \text{m}^{2}$,根据压强公式$p=\frac{F}{S}$可知,压力$F=pS=1.5×10^{7}\ \text{Pa}×2×10^{-6}\ \text{m}^{2}=30\ \text{N}$

20. (11分)新情境 社会热点 (宿迁中考)科技创新助力中国发展,中国桥梁建设领先世界。小明对桥梁建造产生了浓厚的兴趣,想探究桥墩对河底压力与水深度的关系。他找来底面积为 $ 0.01 \, \text{m}^2 $ 的圆柱体,放在水平地面上的压力传感器上,如图甲所示,压力传感器的示数为 $ 100 \, \text{N} $。考虑到不方便测量圆柱体对河底的压力,于是他将圆柱体挂在拉力传感器下方,缓慢向下放至刚好与容器底部接触,如图乙所示。向容器内加水,记录拉力传感器的示数 $ F $ 和水的深度 $ h $,并画出如图丙所示的图像。求：($ g $ 取 $ 10 \, \text{N/kg} $,$ \rho_{\text{水}} = 1 × 10^3 \, \text{kg/m}^3 $)

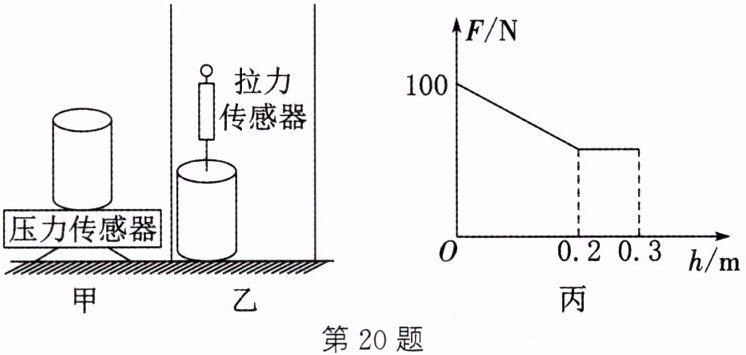
(1)圆柱体的质量。
(2)圆柱体的密度。
(3)取走拉力传感器,圆柱体浸没于水中时对容器底的压强。

答案： （1）圆柱体放于压力传感器上,示数为 100 N,则$G=100\ \text{N}$;圆柱体的质量$m=\frac{G}{g}=\frac{100\ \text{N}}{10\ \text{N/kg}}=10\ \text{kg}$ （2）圆柱体浸没后浮力不变,则拉力不变,由图丙可知,圆柱体的高度$h=0.2\ \text{m}$,体积$V=Sh=0.01\ \text{m}^{2}×0.2\ \text{m}=0.002\ \text{m}^{3}$,圆柱体的密度$\rho=\frac{m}{V}=\frac{10\ \text{kg}}{0.002\ \text{m}^{3}}=5×10^{3}\ \text{kg/m}^{3}$ （3）圆柱体浸没时受到的浮力$F_{\text{浮}}=\rho_{\text{水}}gV_{\text{排}}=\rho_{\text{水}}gV=1×10^{3}\ \text{kg/m}^{3}×10\ \text{N/kg}×0.002\ \text{m}^{3}=20\ \text{N}$,对容器底的压力$F=G-F_{\text{浮}}=100\ \text{N}-20\ \text{N}=80\ \text{N}$,压强$p=\frac{F}{S}=\frac{80\ \text{N}}{0.01\ \text{m}^{2}}=8\ 000\ \text{Pa}$