2025年暑假乐园辽宁师范大学出版社七年级理综
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假乐园辽宁师范大学出版社七年级理综 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第4页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
20. 定义新运算:$\begin{vmatrix}a&b\\c&d\end{vmatrix}=ad - bc$。例如:$\begin{vmatrix}2&a\\-1&b\end{vmatrix}=2× b - a× (-1)=2b + a$。
(1)计算$\begin{vmatrix}10&9x - 2xy - y\\1&xy - y\end{vmatrix}$,其结果为
(2)若$\vert x - 3 + y\vert$与$(xy + 4)^{2}$互为相反数,(1)中结果的值为
(1)计算$\begin{vmatrix}10&9x - 2xy - y\\1&xy - y\end{vmatrix}$,其结果为
12xy - 9y - 9x
,次数为2
,项数为3
。(2)若$\vert x - 3 + y\vert$与$(xy + 4)^{2}$互为相反数,(1)中结果的值为
-75
。
答案:
(1) 由新定义可知,原式 $=10(xy - y)-(9x - 2xy - y)=10xy - 10y - 9x + 2xy + y = 12xy - 9y - 9x$。
12xy - 9y - 9x 的次数为 2,项数为 3。
(2) 因为 $|x - 3 + y|$ 与 $(xy + 4)^{2}$ 互为相反数,所以 $|x - 3 + y|+(xy + 4)^{2}=0$,所以 $x - 3 + y = 0$,$xy + 4 = 0$,则 $x + y = 3$,$xy = -4$,所以
(1) 中原式 $=12xy - 9(x + y)=12 × (-4)-9 × 3 = -75$。
(1) 由新定义可知,原式 $=10(xy - y)-(9x - 2xy - y)=10xy - 10y - 9x + 2xy + y = 12xy - 9y - 9x$。
12xy - 9y - 9x 的次数为 2,项数为 3。
(2) 因为 $|x - 3 + y|$ 与 $(xy + 4)^{2}$ 互为相反数,所以 $|x - 3 + y|+(xy + 4)^{2}=0$,所以 $x - 3 + y = 0$,$xy + 4 = 0$,则 $x + y = 3$,$xy = -4$,所以
(1) 中原式 $=12xy - 9(x + y)=12 × (-4)-9 × 3 = -75$。
21. 和谐广场有一块长为$(3a + b)m$,宽为$(2a + b)m$的长方形地,如图所示,北面两角上各有一块边长为$(a - b)m$的小正方形空地,现要对阴影部分进行绿化。
(1)用含$a$,$b$的式子表示绿化的总面积。(结果写成最简形式)
$(
(2)若$a = 40$,$b = 20$,求绿化的总面积。
$
(1)用含$a$,$b$的式子表示绿化的总面积。(结果写成最简形式)
$(
4a^{2}+9ab - b^{2}
)m^{2}$(2)若$a = 40$,$b = 20$,求绿化的总面积。
$
13200
m^{2}$
答案:
(1) 绿化的总面积为 $(3a + b)(2a + b)-2(a - b)^{2}=4a^{2}+9ab - b^{2}(m^{2})$。
(2) 当 $a = 40$,$b = 20$ 时,绿化的总面积为 $4 × 40^{2}+9 × 40 × 20 - 20^{2}=13200(m^{2})$。
(1) 绿化的总面积为 $(3a + b)(2a + b)-2(a - b)^{2}=4a^{2}+9ab - b^{2}(m^{2})$。
(2) 当 $a = 40$,$b = 20$ 时,绿化的总面积为 $4 × 40^{2}+9 × 40 × 20 - 20^{2}=13200(m^{2})$。
22.【知识技能】
已知:$(a + b)^{2}=a^{2}+b^{2}+2ab$,$(a - b)^{2}=a^{2}+b^{2}-2ab$。
填空:(1)①$a^{2}+b^{2}=(a + b)^{2}-$
【数学理解】
若$x$满足$(5 - x)(x - 2)=2$,求$(5 - x)^{2}+(x - 2)^{2}$的值。
解:设$5 - x = a$,$x - 2 = b$,则$(5 - x)(x - 2)=ab = 2$,$a + b=(5 - x)+(x - 2)=3$,
所以$(5 - x)^{2}+(x - 2)^{2}=a^{2}+b^{2}=(a + b)^{2}-2ab = 3^{2}-2× 2 = 5$。
【解决问题】
(2)①若$x$满足$(7 - x)(x - 3)=3$,则$(7 - x)^{2}+(x - 3)^{2}=$
②若$x$满足$(x + 1)^{2}+(x - 3)^{2}=26$,求$(x + 1)(x - 3)$的值。
解:设 $x + 1 = m$,$x - 3 = n$,则 $m - n = 4$,$m^{2}+n^{2}=(x + 1)^{2}+(x - 3)^{2}=26$,所以 $(x + 1)(x - 3)=mn=\frac{(m - n)^{2}-(m^{2}+n^{2})}{-2}=$
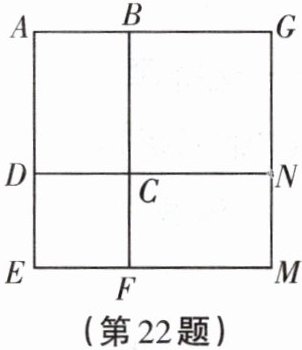
解:由题意,得 $x(x + 1)=6$。设 $AB = a$,$AD = b$,则 $a - b = x-(x + 1)=-1$,$ab = x(x + 1)=6$,所以 $S_{正方形AEMG}=AE^{2}=(a + b)^{2}=(a - b)^{2}+4ab=(-1)^{2}+4 × 6 =$
已知:$(a + b)^{2}=a^{2}+b^{2}+2ab$,$(a - b)^{2}=a^{2}+b^{2}-2ab$。
填空:(1)①$a^{2}+b^{2}=(a + b)^{2}-$
$2ab$
;②$(a + b)^{2}-(a - b)^{2}=$$4ab$
。【数学理解】
若$x$满足$(5 - x)(x - 2)=2$,求$(5 - x)^{2}+(x - 2)^{2}$的值。
解:设$5 - x = a$,$x - 2 = b$,则$(5 - x)(x - 2)=ab = 2$,$a + b=(5 - x)+(x - 2)=3$,
所以$(5 - x)^{2}+(x - 2)^{2}=a^{2}+b^{2}=(a + b)^{2}-2ab = 3^{2}-2× 2 = 5$。
【解决问题】
(2)①若$x$满足$(7 - x)(x - 3)=3$,则$(7 - x)^{2}+(x - 3)^{2}=$
10
。②若$x$满足$(x + 1)^{2}+(x - 3)^{2}=26$,求$(x + 1)(x - 3)$的值。
解:设 $x + 1 = m$,$x - 3 = n$,则 $m - n = 4$,$m^{2}+n^{2}=(x + 1)^{2}+(x - 3)^{2}=26$,所以 $(x + 1)(x - 3)=mn=\frac{(m - n)^{2}-(m^{2}+n^{2})}{-2}=$
5
。 ③如图,已知正方形$AEMG$被分割成4个部分,其中四边形$CDEF$与$BCNG$为正方形,若$AB = x$,$AD = x + 1$,四边形$ABCD$的面积为6,求正方形$AEMG$的面积。
解:由题意,得 $x(x + 1)=6$。设 $AB = a$,$AD = b$,则 $a - b = x-(x + 1)=-1$,$ab = x(x + 1)=6$,所以 $S_{正方形AEMG}=AE^{2}=(a + b)^{2}=(a - b)^{2}+4ab=(-1)^{2}+4 × 6 =$
25
。
答案:
(1) ① $2ab$ ② $4ab$
(2) ① 10 ② 设 $x + 1 = m$,$x - 3 = n$,则 $m - n = 4$,$m^{2}+n^{2}=(x + 1)^{2}+(x - 3)^{2}=26$,所以 $(x + 1)(x - 3)=mn=\frac{(m - n)^{2}-(m^{2}+n^{2})}{-2}=5$。 ③ 由题意,得 $x(x + 1)=6$。设 $AB = a$,$AD = b$,则 $a - b = x-(x + 1)=-1$,$ab = x(x + 1)=6$,所以 $S_{正方形AEMG}=AE^{2}=(a + b)^{2}=(a - b)^{2}+4ab=(-1)^{2}+4 × 6 = 25$。
(1) ① $2ab$ ② $4ab$
(2) ① 10 ② 设 $x + 1 = m$,$x - 3 = n$,则 $m - n = 4$,$m^{2}+n^{2}=(x + 1)^{2}+(x - 3)^{2}=26$,所以 $(x + 1)(x - 3)=mn=\frac{(m - n)^{2}-(m^{2}+n^{2})}{-2}=5$。 ③ 由题意,得 $x(x + 1)=6$。设 $AB = a$,$AD = b$,则 $a - b = x-(x + 1)=-1$,$ab = x(x + 1)=6$,所以 $S_{正方形AEMG}=AE^{2}=(a + b)^{2}=(a - b)^{2}+4ab=(-1)^{2}+4 × 6 = 25$。
查看更多完整答案,请扫码查看


