《2025年暑假作业内蒙古大学出版社七年级数学》

10. 如图,直线$a$,$b被直线c$所截,$\angle 1= \angle 2= \angle 3$,下列说法错误的是(D)
A.$\angle 1= 90^{\circ}$
B.$b\perp c$
C.$a// b$
D.$a\perp b$

答案： 解：
∵∠1+∠2=180°（平角定义），∠1=∠2，
∴∠1=∠2=90°，A正确；
∵∠2=∠3，∠2=90°，
∴∠3=90°，即b⊥c，B正确；
∵∠1=∠3=90°，
∴a//b（同位角相等，两直线平行），C正确；
∵a//b，∠1=90°，
∴a与b不垂直，D错误。
结论：D

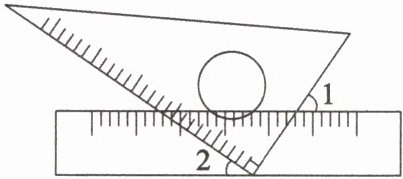
11. 小明将一块直角三角板摆放在直尺上,如图,若$\angle 1= 55^{\circ}$,则$\angle 2$的度数为(B)

A.$25^{\circ}$
B.$35^{\circ}$
C.$45^{\circ}$
D.$55^{\circ}$

答案： 解：如图，因为直尺的两边互相平行，所以∠1的同位角等于∠1=55°。
直角三角板的直角为90°，则∠2=90°-55°=35°。
答案：B

12. 在平面直角坐标系中,对于点$P(x,y)$,我们把点$P'(-y+1,x+1)$叫做点$P$的伴随点. 已知点$A_1$的伴随点为$A_2$,点$A_2$的伴随点为$A_3$,点$A_3$的伴随点为$A_4$,……. 若点$A_1$的坐标为$(2,4)$,则点$A_{2026}$的坐标为(A)
A.$(-3,3)$
B.$(-2,-2)$
C.$(3,-1)$
D.$(2,4)$

答案： 解：已知点$A_1$的坐标为$(2,4)$。
根据伴随点定义：$P'( -y + 1, x + 1)$。
$A_2$为$A_1$的伴随点：$x=2$，$y=4$，则$A_2(-4 + 1, 2 + 1)=(-3,3)$；
$A_3$为$A_2$的伴随点：$x=-3$，$y=3$，则$A_3(-3 + 1, -3 + 1)=(-2,-2)$；
$A_4$为$A_3$的伴随点：$x=-2$，$y=-2$，则$A_4(2 + 1, -2 + 1)=(3,-1)$；
$A_5$为$A_4$的伴随点：$x=3$，$y=-1$，则$A_5(1 + 1, 3 + 1)=(2,4)$。
由此可得，点的坐标以$A_1(2,4)$，$A_2(-3,3)$，$A_3(-2,-2)$，$A_4(3,-1)$为周期循环，周期为$4$。
因为$2026÷4=506\cdots\cdots2$，余数为$2$，所以$A_{2026}$与$A_2$坐标相同，为$(-3,3)$。
答案：A

13. (1)计算：$\sqrt{4}=$2.
(2)$8$的立方根是2.

答案：
(1) 2
(2) 2

14. 如图,直线$a// b$,若$\angle 1= 28^{\circ}$,则$\angle 2= $$152^{\circ}$.

答案： 解：因为直线$a // b$，$\angle 1 = 28^{\circ}$，
所以$\angle 1$与$\angle 2$是同旁内角，
根据两直线平行，同旁内角互补，
可得$\angle 1 + \angle 2 = 180^{\circ}$，
所以$\angle 2 = 180^{\circ} - \angle 1 = 180^{\circ} - 28^{\circ} = 152^{\circ}$。
$152^{\circ}$

15. 如图,在数轴上,点$A表示\sqrt{3}$,点$B与点A$位于原点的两侧,且与原点的距离相等. 则点$B$表示的数是$-\sqrt{3}$.

答案： 解：因为点$A$表示$\sqrt{3}$，点$B$与点$A$位于原点两侧且与原点距离相等，所以点$B$表示的数是$-\sqrt{3}$。
$-\sqrt{3}$

16. 如图,将直角三角形$ABC沿着点B到C的方向平移到三角形DEF$的位置,$AB= 9$,$DO= 4$,平移距离为$6$,则阴影部分面积为______.

42

答案： 解：由平移性质得，$DE=AB=9$，$BE=6$，$S_{\triangle ABC}=S_{\triangle DEF}$。
$OE=DE-DO=9-4=5$。
$S_{\text{阴影}}=S_{\triangle DEF}-S_{\triangle OEC}=S_{\triangle ABC}-S_{\triangle OEC}=S_{\text{梯形}ABEO}$。
$S_{\text{梯形}ABEO}=\frac{1}{2}(AB+OE)× BE=\frac{1}{2}×(9+5)×6=42$。
42

17. 用“$*$”表示一种新运算：对于任意正实数$a$,$b$,都有$a*b= \sqrt{b}+1$. 例如$8*9= \sqrt{9}+1= 4$,那么$15*196= $15,$m*(m*16)= $√5 + 1.

答案： 15*196 = √196 + 1 = 14 + 1 = 15
m*(m*16) = m*(√16 + 1) = m*5 = √5 + 1
15，√5 + 1

18. 五子棋是一种两人对弈的棋类游戏,规则是：在正方形棋盘中,由黑方先行,白方后行,轮流弈子,下在棋盘横线与竖线的交叉点上,直到某一方首先在任一方向(横向、竖向或者是斜着的方向)上连成五子者为胜. 如图,这一部分棋盘是两个五子棋爱好者的对弈图. 观察棋盘,以点$O$为原点,在棋盘上建立平面直角坐标系,将每个棋子看成一个点. 若黑子$A的坐标为(7,5)$,为了不让白方获胜,此时黑方应该下在坐标为$(3,7)$或$(7,3)$的位置处.

答案： 解：为了不让白方获胜，黑方应阻止白方在任一方向连成五子。观察棋盘，白方在横向、竖向或斜向可能形成四子连线的位置需被阻断。经分析，此时黑方应该下在坐标为$(3,7)$或$(7,3)$的位置处。
$(3,7)$；$(7,3)$

19. 计算：(1)$|-3|-\sqrt{16}+\sqrt[3]{8}+(-2)^2$；
(2)$2×\sqrt{(-\frac{1}{2})^2}+\sqrt{25}-\sqrt[3]{-27}$.

答案：
(1) 解：原式 $=3 - 4 + 2 + 4 = 5$
(2) 解：原式 $=2×\frac{1}{2} + 5 + 3 = 1 + 5 + 3 = 9$