《2025年暑假园地知识出版社五年级数学人教版》

1. 一个带盖的长方体木箱,体积是0.576立方米,它的长是12分米,宽是8分米,做这样一个木箱至少要用木板多少平方米？ 

答案： 解：
1. 首先进行单位换算：
已知$1$分米$ = 0.1$米，则长$a = 12$分米$=12×0.1 = 1.2$米，宽$b = 8$分米$=8×0.1 = 0.8$米。
根据长方体体积公式$V=a× b× h$（$V$是体积，$a$是长，$b$是宽，$h$是高），可得高$h=\frac{V}{a× b}$。
把$V = 0.576$立方米，$a = 1.2$米，$b = 0.8$米代入公式，$h=\frac{0.576}{1.2×0.8}=\frac{0.576}{0.96}=0.6$米。
2. 然后求长方体的表面积：
长方体表面积公式$S=(a× b + a× h + b× h)×2$。
把$a = 1.2$米，$b = 0.8$米，$h = 0.6$米代入公式：
$S=(1.2×0.8 + 1.2×0.6+0.8×0.6)×2$。
先计算括号内的值：$1.2×0.8 = 0.96$，$1.2×0.6 = 0.72$，$0.8×0.6 = 0.48$。
则$1.2×0.8 + 1.2×0.6+0.8×0.6=0.96 + 0.72+0.48=2.16$。
再计算$S = 2.16×2=4.32$平方米。
答：做这样一个木箱至少要用木板$4.32$平方米。

2. 妈妈制作了酸梅汤,盛放在底面是正方形的保鲜盒中。如图,现在要将它倒入另一个长方体保鲜盒中,此时酸梅汤的高度是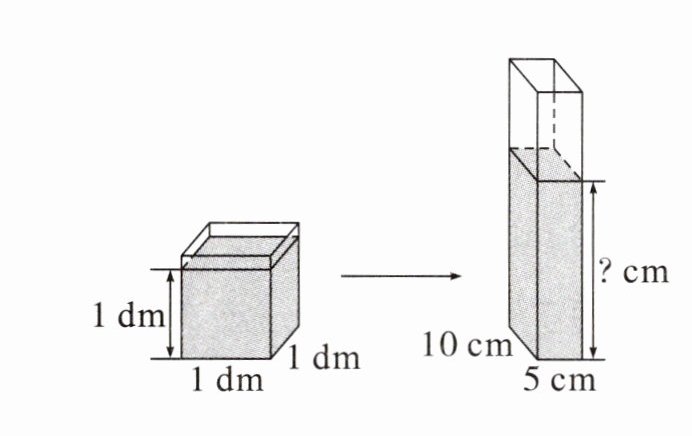20厘米？

答案： 1. 首先统一单位：
已知$1dm = 10cm$。
根据正方体体积公式$V=a^{3}$（$a$为正方体棱长），原来酸梅汤在底面是正方形（棱长$a = 10cm$）的保鲜盒中，酸梅汤高度$h_1 = 10cm$，则酸梅汤体积$V=10×10×10$（$cm^{3}$）。
2. 然后根据长方体体积公式$V = S× h$（$S$为长方体底面积，$h$为高）求倒入长方体保鲜盒后的高度：
长方体保鲜盒底面积$S = 10×5$（$cm^{2}$）。
因为酸梅汤体积不变，由$V = S× h$可得$h=\frac{V}{S}$。
把$V = 10×10×10$，$S = 10×5$代入公式，$h=\frac{10×10×10}{10×5}$。
先计算分子$10×10×10 = 1000$，分母$10×5 = 50$，则$h=\frac{1000}{50}=20$（$cm$）。
解：酸梅汤体积$V = 10×10×10$（$cm^{3}$），长方体保鲜盒底面积$S = 10×5$（$cm^{2}$），根据$h=\frac{V}{S}$，$h=\frac{10×10×10}{10×5}=20$（$cm$）。
答：此时酸梅汤的高度是$20$厘米。

3. 一个长方体木块,从下部和上部截去高分别是2cm和3cm的长方体后,变成一个正方体,表面积减少了$120cm^{2}$。原来长方体木块的体积是多少立方厘米？
 

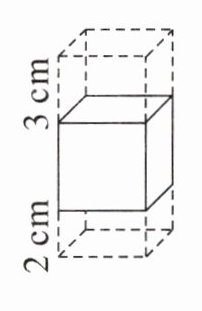
答案： 解：
1. 分析表面积减少的部分：
截去上下两个长方体后，表面积减少的部分是$4$个相同的以原来长方体底面边长为长，$(2 + 3)$为宽的长方形的面积之和。
设正方体的棱长为$x cm$，则可列出方程$4× x×(2 + 3)=120$。
2. 求解正方体的棱长$x$：
化简方程$4× x×(2 + 3)=120$，即$20x = 120$，解得$x = 6$。
3. 计算原来长方体的高：
原来长方体的高为$6 + 2+3=11cm$。
4. 计算原来长方体的体积：
根据长方体体积公式$V = a× b× h$（这里$a = b=x = 6$，$h = 11$），则$V=6×6×11$。
$V = 396cm^{3}$。
答：原来长方体木块的体积是$396cm^{3}$。