10. 当 k 为何值时,函数 $ y = ( k - 1 ) x ^ { k ^ { 2 } } $ 是正比例函数?
答案:
解:由题意得$\begin{cases} k - 1 \neq 0, \\ k^2 = 1, \end{cases}$解得$k = -1$。故当$k = -1$时,$y = (k - 1)x^{k^2}$是正比例函数。
11. 下列四组点中,可以在同一个正比例函数图象上的一组点是(
A.$ ( 2 , - 3 ) $,$ ( - 4 , 6 ) $
B.$ ( - 2 , 3 ) $,$ ( 4 , 6 ) $
C.$ ( - 2 , - 3 ) $,$ ( 4 , - 6 ) $
D.$ ( 2 , 3 ) $,$ ( - 4 , 6 ) $
A
)A.$ ( 2 , - 3 ) $,$ ( - 4 , 6 ) $
B.$ ( - 2 , 3 ) $,$ ( 4 , 6 ) $
C.$ ( - 2 , - 3 ) $,$ ( 4 , - 6 ) $
D.$ ( 2 , 3 ) $,$ ( - 4 , 6 ) $
答案:
A
12. 已知正比例函数 $ y = ( 2 m - 1 ) x $ 的图象上有两点 $ A ( a _ { 1 } , b _ { 1 } ) $,$ B ( a _ { 2 } , b _ { 2 } ) $,当 $ a _ { 1 } < a _ { 2 } $ 时,有 $ b _ { 1 } > b _ { 2 } $,则 m 的取值范围是(
A.$ m < \frac { 1 } { 2 } $
B.$ m > \frac { 1 } { 2 } $
C.$ m < 2 $
D.$ m > 0 $
A
)A.$ m < \frac { 1 } { 2 } $
B.$ m > \frac { 1 } { 2 } $
C.$ m < 2 $
D.$ m > 0 $
答案:
A
13. 如图,三个正比例函数的图象分别对应的解析式是① $ y = a x $,② $ y = b x $,③ $ y = c x $,则 a,b,c 的大小关系是(
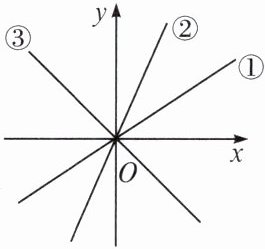
A.$ a > b > c $
B.$ c > b > a $
C.$ b > a > c $
D.$ b > c > a $
C
)
A.$ a > b > c $
B.$ c > b > a $
C.$ b > a > c $
D.$ b > c > a $
答案:
C
14. 已知正比例函数 $ y = ( 2 m - 1 ) x ^ { m ^ { 2 } - 3 } $,且 y 随着 x 的增大而减小,求 m 的值.
答案:
解:由$m^2 - 3 = 1$,得$m^2 = 4$,即$m = \pm 2$。
又$y$随$x$的增大而减小,所以$2m - 1 < 0$,即$m < \frac{1}{2}$。故$m = -2$。
又$y$随$x$的增大而减小,所以$2m - 1 < 0$,即$m < \frac{1}{2}$。故$m = -2$。
查看更多完整答案,请扫码查看


