《2025年暑假作业八年级数学内蒙古教育出版社》

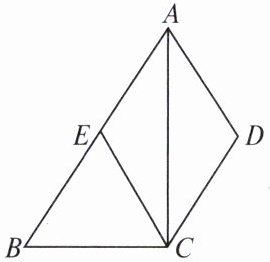
15. 在四边形ABCD中,$AB// CD$,AC平分$\angle BAD$,$CE// AD$交AB于点E.
(1)求证:四边形AECD是菱形;
(2)若点E是AB的中点,试判断$\triangle ABC$的形状,并说明理由.

(1)证明：$\because AB// CD,\therefore AE// CD.$
又$CE// AD,$
$\therefore$四边形$AECD$是平行四边形.
$\because AC$平分$∠BAD,\therefore ∠CAE=∠CAD.$
又$AD// CE,\therefore ∠ACE=∠CAD.$
$\therefore ∠ACE=∠CAE.\therefore AE=CE.$
$\therefore$四边形$AECD$是菱形.
(2)解：$\triangle ABC$是直角三角形.
理由：$\because E$是$AB$中点,$\therefore AE=BE.$
又$AE=CE,\therefore BE=CE.\therefore ∠B=∠BCE.$
$\because ∠B+∠BCA+∠BAC=180^{\circ },$
$\therefore 2∠BCE+2∠ACE=180^{\circ }.$
$\therefore ∠BCE+∠ACE=90^{\circ }.$
即$∠ACB=90^{\circ },\therefore \triangle ABC$是直角三角形.

答案：
(1)证明：$\because AB// CD,\therefore AE// CD.$
又$CE// AD,$
$\therefore$四边形$AECD$是平行四边形.
$\because AC$平分$∠BAD,\therefore ∠CAE=∠CAD.$
又$AD// CE,\therefore ∠ACE=∠CAD.$
$\therefore ∠ACE=∠CAE.\therefore AE=CE.$
$\therefore$四边形$AECD$是菱形.
(2)解：$\triangle ABC$是直角三角形.
理由：$\because E$是$AB$中点,$\therefore AE=BE.$
又$AE=CE,\therefore BE=CE.\therefore ∠B=∠BCE.$
$\because ∠B+∠BCA+∠BAC=180^{\circ },$
$\therefore 2∠BCE+2∠ACE=180^{\circ }.$
$\therefore ∠BCE+∠ACE=90^{\circ }.$
即$∠ACB=90^{\circ },\therefore \triangle ABC$是直角三角形.

16. 将矩形ABCD折叠,使A,C重合,折痕交BC于点E,交AD于点F.
(1)求证:四边形AECF为菱形;
(2)若$AB= 12$,$BC= 18$,求菱形AECF的边长.

(1)证明：$\because$将矩形$ABCD$折叠，使$A$，$C$重合，折痕为$EF$，
$\therefore OA=OC,EF⊥AC,EA=EC.$
$\because AD// BC,\therefore ∠FAC=∠ECA.$
在$\triangle AOF$和$\triangle COE$中，
$\because ∠FAO=∠ECO,AO=CO,∠AOF=∠COE,$
$\therefore \triangle AOF\cong \triangle COE(ASA).\therefore OF=OE.$
$\because OA=OC,\therefore$四边形$AECF$为平行四边形.
$\because AC⊥EF,\therefore$四边形$AECF$为菱形.
(2)解：设菱形的边长为$x$，则$BE=BC-CE=18-x,AE=x.$
在$Rt\triangle ABE$中，$\because BE^{2}+AB^{2}=AE^{2},$
$\therefore (18-x)^{2}+12^{2}=x^{2}$，解得$x=$13.
$\therefore$菱形$AECF$的边长为13.

答案：
(1)证明：$\because$将矩形$ABCD$折叠，使$A$，$C$重合，折痕为$EF$，
$\therefore OA=OC,EF⊥AC,EA=EC.$
$\because AD// BC,\therefore ∠FAC=∠ECA.$
在$\triangle AOF$和$\triangle COE$中，
$\because ∠FAO=∠ECO,AO=CO,∠AOF=∠COE,$
$\therefore \triangle AOF\cong \triangle COE(ASA).\therefore OF=OE.$
$\because OA=OC,\therefore$四边形$AECF$为平行四边形.
$\because AC⊥EF,\therefore$四边形$AECF$为菱形.
(2)解：设菱形的边长为$x$，则$BE=BC-CE=18-x,AE=x.$
在$Rt\triangle ABE$中，$\because BE^{2}+AB^{2}=AE^{2},$
$\therefore (18-x)^{2}+12^{2}=x^{2}$，解得$x=13.$
$\therefore$菱形$AECF$的边长为$13$.