2025年新活力总动员暑假八年级物理人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新活力总动员暑假八年级物理人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1.(长春中考)如图所示是《天工开物》中记载的南方独轮推车。人推车前进的过程中(

A.人对车不做功
B.车是定滑轮
C.车是费力杠杆
D.车是省力杠杆
D
)
A.人对车不做功
B.车是定滑轮
C.车是费力杠杆
D.车是省力杠杆
答案:
D
2. 小华学习了简单机械后,归纳了几条“规律”。其中总结正确的是(
A.任何机械都不省功
B.机械的有用功越多,机械效率一定越大
C.机械的功率越大,机械效率越大
D.机械的功率越大,做功一定越多
A
)A.任何机械都不省功
B.机械的有用功越多,机械效率一定越大
C.机械的功率越大,机械效率越大
D.机械的功率越大,做功一定越多
答案:
【解析】:
本题主要考查对简单机械的功能、机械效率以及功率的理解。
A选项,根据功的原理,使用任何机械都不省功,这是因为使用机械时,动力对机械所做的功总等于机械克服阻力所做的功,即使用任何机械都不省功,所以A选项是正确的。
B选项,机械效率是指有用功占总功的比例,即$\eta = \frac{W_{有用}}{W_{总}}$。从这个公式可以看出,机械效率不仅与有用功有关,还与总功有关。因此,即使有用功增多,如果总功也相应增多,机械效率并不一定增大。所以B选项是错误的。
C选项,功率是表示做功快慢的物理量,而机械效率是有用功占总功的比例。两者没有必然的联系。因此,功率大的机械,机械效率并不一定大。所以C选项是错误的。
D选项,功率是表示做功快慢的物理量,它等于功除以时间,即$P = \frac{W}{t}$。从这个公式可以看出,功率大的机械,在相同时间内做的功多,但如果时间不确定,那么做功的多少也无法确定。所以D选项是错误的。
综上所述,只有A选项是正确的。
【答案】:A。
本题主要考查对简单机械的功能、机械效率以及功率的理解。
A选项,根据功的原理,使用任何机械都不省功,这是因为使用机械时,动力对机械所做的功总等于机械克服阻力所做的功,即使用任何机械都不省功,所以A选项是正确的。
B选项,机械效率是指有用功占总功的比例,即$\eta = \frac{W_{有用}}{W_{总}}$。从这个公式可以看出,机械效率不仅与有用功有关,还与总功有关。因此,即使有用功增多,如果总功也相应增多,机械效率并不一定增大。所以B选项是错误的。
C选项,功率是表示做功快慢的物理量,而机械效率是有用功占总功的比例。两者没有必然的联系。因此,功率大的机械,机械效率并不一定大。所以C选项是错误的。
D选项,功率是表示做功快慢的物理量,它等于功除以时间,即$P = \frac{W}{t}$。从这个公式可以看出,功率大的机械,在相同时间内做的功多,但如果时间不确定,那么做功的多少也无法确定。所以D选项是错误的。
综上所述,只有A选项是正确的。
【答案】:A。
3.(黄石中考)下列关于简单机械在实际应用中的说法正确的是(
A.指甲剪是省力省功的机械
B.定滑轮不省力,但能改变力的方向
C.滑轮组既省力,又省距离,还省功
D.斜面的机械效率可以达到100%
B
)A.指甲剪是省力省功的机械
B.定滑轮不省力,但能改变力的方向
C.滑轮组既省力,又省距离,还省功
D.斜面的机械效率可以达到100%
答案:
【解析】:
本题主要考查简单机械在实际应用中的性质和特点,包括指甲剪、定滑轮、滑轮组以及斜面的工作原理和机械效率。
A选项,使用任何机械都不能省功,因为功是能量转化的量度,省力必然费距离,省距离必然费力,所以指甲剪不可能是省力又省功的机械,故A错误。
B选项,定滑轮实质上是等臂杠杆,使用定滑轮不省力,但可以改变力的方向,故B正确。
C选项,滑轮组可以省力,因为滑轮组有动滑轮,可以省力,但同时需要费距离,而且使用任何机械都不能省功,故C错误。
D选项,使用任何机械都要做额外功,所以有用功和总功的比值一般小于$1$,即机械效率小于$100\%$,故D错误。
【答案】:B。
本题主要考查简单机械在实际应用中的性质和特点,包括指甲剪、定滑轮、滑轮组以及斜面的工作原理和机械效率。
A选项,使用任何机械都不能省功,因为功是能量转化的量度,省力必然费距离,省距离必然费力,所以指甲剪不可能是省力又省功的机械,故A错误。
B选项,定滑轮实质上是等臂杠杆,使用定滑轮不省力,但可以改变力的方向,故B正确。
C选项,滑轮组可以省力,因为滑轮组有动滑轮,可以省力,但同时需要费距离,而且使用任何机械都不能省功,故C错误。
D选项,使用任何机械都要做额外功,所以有用功和总功的比值一般小于$1$,即机械效率小于$100\%$,故D错误。
【答案】:B。
4.(聊城中考)如图所示,用相同的滑轮安装成甲、乙两种装置,分别将A、B两物体匀速向上提升,若所用拉力大小相等,绳端在相同时间内移动了相同的距离。不计绳重和摩擦,下列说法正确的是(
A.两物体上升的速度相同
B.两种装置的机械效率相等
C.两次提升物体所做的有用功相等
D.两种装置中拉力做功的功率相等
D
)A.两物体上升的速度相同
B.两种装置的机械效率相等
C.两次提升物体所做的有用功相等
D.两种装置中拉力做功的功率相等
答案:
解:
由图可知,甲为定滑轮($n_甲=1$),乙为动滑轮($n_乙=2$)。
A. 绳端移动距离$s = nh$,物体上升高度$h = \frac{s}{n}$,相同时间内$s$相同,则物体上升速度$v = \frac{h}{t} = \frac{s}{nt}$。
$v_甲 = \frac{s}{n_甲t} = \frac{s}{t}$,$v_乙 = \frac{s}{n_乙t} = \frac{s}{2t}$,$v_甲 \neq v_乙$,A错误。
B. 不计绳重和摩擦,拉力$F_甲 = G_A$,$F_乙 = \frac{G_B + G_动}{2}$。因$F_甲 = F_乙 = F$,则$G_A = F$,$G_B = 2F - G_动$。
机械效率$\eta = \frac{W_有}{W_总} = \frac{Gh}{Fs} = \frac{Gh}{Fnh} = \frac{G}{nF}$。
$\eta_甲 = \frac{G_A}{n_甲F} = \frac{F}{1 × F} = 1$,$\eta_乙 = \frac{G_B}{n_乙F} = \frac{2F - G_动}{2F} < 1$,$\eta_甲 \neq \eta_乙$,B错误。
C. 有用功$W_有 = Gh$,$h_甲 = s$,$h_乙 = \frac{s}{2}$。
$W_{有甲} = G_Ah_甲 = Fs$,$W_{有乙} = G_Bh_乙 = (2F - G_动)\frac{s}{2} = Fs - \frac{G_动s}{2} < Fs$,$W_{有甲} \neq W_{有乙}$,C错误。
D. 拉力做功功率$P = \frac{W_总}{t} = \frac{Fs}{t}$,因$F$、$s$、$t$均相同,则$P_甲 = P_乙$,D正确。
答案:D
由图可知,甲为定滑轮($n_甲=1$),乙为动滑轮($n_乙=2$)。
A. 绳端移动距离$s = nh$,物体上升高度$h = \frac{s}{n}$,相同时间内$s$相同,则物体上升速度$v = \frac{h}{t} = \frac{s}{nt}$。
$v_甲 = \frac{s}{n_甲t} = \frac{s}{t}$,$v_乙 = \frac{s}{n_乙t} = \frac{s}{2t}$,$v_甲 \neq v_乙$,A错误。
B. 不计绳重和摩擦,拉力$F_甲 = G_A$,$F_乙 = \frac{G_B + G_动}{2}$。因$F_甲 = F_乙 = F$,则$G_A = F$,$G_B = 2F - G_动$。
机械效率$\eta = \frac{W_有}{W_总} = \frac{Gh}{Fs} = \frac{Gh}{Fnh} = \frac{G}{nF}$。
$\eta_甲 = \frac{G_A}{n_甲F} = \frac{F}{1 × F} = 1$,$\eta_乙 = \frac{G_B}{n_乙F} = \frac{2F - G_动}{2F} < 1$,$\eta_甲 \neq \eta_乙$,B错误。
C. 有用功$W_有 = Gh$,$h_甲 = s$,$h_乙 = \frac{s}{2}$。
$W_{有甲} = G_Ah_甲 = Fs$,$W_{有乙} = G_Bh_乙 = (2F - G_动)\frac{s}{2} = Fs - \frac{G_动s}{2} < Fs$,$W_{有甲} \neq W_{有乙}$,C错误。
D. 拉力做功功率$P = \frac{W_总}{t} = \frac{Fs}{t}$,因$F$、$s$、$t$均相同,则$P_甲 = P_乙$,D正确。
答案:D
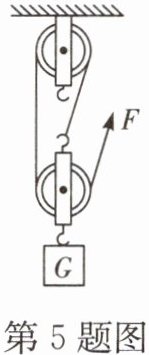
5.(永州中考)如图所示,用F= 10N的拉力使重物匀速上升0.1m,已知物体的重力为27N(忽略绳子与滑轮的摩擦及绳子的重力),下列说法正确的是(
A.绳子末端移动的距离是0.2m
B.拉力做的功是2.7J
C.滑轮组的机械效率是90%
D.动滑轮的重力是1N
C
)
A.绳子末端移动的距离是0.2m
B.拉力做的功是2.7J
C.滑轮组的机械效率是90%
D.动滑轮的重力是1N
答案:
【解析】:本题主要考查滑轮组的特点、功的计算、机械效率的计算以及动滑轮重力的计算。
A选项:需要判断绳子末端移动的距离。由图可知,承担物重的绳子段数$n = 3$。根据滑轮组的特点,绳子末端移动的距离$s$与物体上升的高度$h$的关系为$s = nh$。已知物体上升的高度$h = 0.1m$,则绳子末端移动的距离$s = 3×0.1m = 0.3m$,所以A选项错误。
B选项:计算拉力做的功,即总功$W_{总}$。根据功的计算公式$W = Fs$,已知拉力$F = 10N$,绳子末端移动的距离$s = 0.3m$,则拉力做的功$W_{总}=Fs = 10N×0.3m = 3J$,所以B选项错误。
C选项:计算滑轮组的机械效率$\eta$。先计算有用功$W_{有}$,根据公式$W_{有}=Gh$,已知物体重力$G = 27N$,物体上升的高度$h = 0.1m$,则有用功$W_{有}=27N×0.1m = 2.7J$。再根据机械效率的计算公式$\eta=\frac{W_{有}}{W_{总}}×100\%$,将$W_{有}= 2.7J$,$W_{总}= 3J$代入可得$\eta=\frac{2.7J}{3J}×100\% = 90\%$,所以C选项正确。
D选项:计算动滑轮的重力$G_{动}$。在不计绳子重及摩擦的情况下,根据公式$F=\frac{1}{n}(G + G_{动})$,可得$G_{动}=nF - G$。将$n = 3$,$F = 10N$,$G = 27N$代入可得$G_{动}=3×10N - 27N = 3N$,所以D选项错误。
【答案】:C
A选项:需要判断绳子末端移动的距离。由图可知,承担物重的绳子段数$n = 3$。根据滑轮组的特点,绳子末端移动的距离$s$与物体上升的高度$h$的关系为$s = nh$。已知物体上升的高度$h = 0.1m$,则绳子末端移动的距离$s = 3×0.1m = 0.3m$,所以A选项错误。
B选项:计算拉力做的功,即总功$W_{总}$。根据功的计算公式$W = Fs$,已知拉力$F = 10N$,绳子末端移动的距离$s = 0.3m$,则拉力做的功$W_{总}=Fs = 10N×0.3m = 3J$,所以B选项错误。
C选项:计算滑轮组的机械效率$\eta$。先计算有用功$W_{有}$,根据公式$W_{有}=Gh$,已知物体重力$G = 27N$,物体上升的高度$h = 0.1m$,则有用功$W_{有}=27N×0.1m = 2.7J$。再根据机械效率的计算公式$\eta=\frac{W_{有}}{W_{总}}×100\%$,将$W_{有}= 2.7J$,$W_{总}= 3J$代入可得$\eta=\frac{2.7J}{3J}×100\% = 90\%$,所以C选项正确。
D选项:计算动滑轮的重力$G_{动}$。在不计绳子重及摩擦的情况下,根据公式$F=\frac{1}{n}(G + G_{动})$,可得$G_{动}=nF - G$。将$n = 3$,$F = 10N$,$G = 27N$代入可得$G_{动}=3×10N - 27N = 3N$,所以D选项错误。
【答案】:C
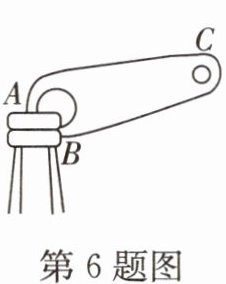
6. 如图所示的起瓶器,它属于
省力
(填“省力”或“费力”)杠杆,在A、B两点中,A
点是支点,开瓶盖时在C点处施加向上
(填“向上”或“向下”)的力。
答案:
【解析】:本题主要考查杠杆原理及其分类,以及杠杆支点和施力方向的判断。
首先,我们需要明确杠杆的基本定义和分类。杠杆是一个能在力的作用下绕着固定点转动的硬棒。根据动力臂和阻力臂的长度关系,杠杆可以分为省力杠杆、费力杠杆和等臂杠杆。在本题中,起瓶器就是一个杠杆的应用实例。
接下来,我们分析起瓶器的结构和工作原理。起瓶器在打开瓶盖时,会绕着某一点转动,这一点就是杠杆的支点。观察图片,我们可以看到起瓶器的A点在打开瓶盖时作为转动点,因此A点是支点。
然后,我们判断起瓶器是省力杠杆还是费力杠杆。省力杠杆的特点是动力臂大于阻力臂,即施加的力较小就能产生较大的效果。在起瓶器中,动力作用在C点,阻力作用在瓶盖上(可以看作作用在B点附近),由于动力臂(从A点到C点的距离)大于阻力臂(从A点到瓶盖边缘的距离),因此起瓶器是省力杠杆。
最后,我们确定在C点施加力的方向。由于起瓶器是省力杠杆,且动力臂大于阻力臂,根据杠杆原理,我们知道在动力臂上施加的力应该使杠杆绕着支点逆时针转动,从而打开瓶盖。因此,在C点应该施加一个向上的力。
【答案】:省力;A;向上。
首先,我们需要明确杠杆的基本定义和分类。杠杆是一个能在力的作用下绕着固定点转动的硬棒。根据动力臂和阻力臂的长度关系,杠杆可以分为省力杠杆、费力杠杆和等臂杠杆。在本题中,起瓶器就是一个杠杆的应用实例。
接下来,我们分析起瓶器的结构和工作原理。起瓶器在打开瓶盖时,会绕着某一点转动,这一点就是杠杆的支点。观察图片,我们可以看到起瓶器的A点在打开瓶盖时作为转动点,因此A点是支点。
然后,我们判断起瓶器是省力杠杆还是费力杠杆。省力杠杆的特点是动力臂大于阻力臂,即施加的力较小就能产生较大的效果。在起瓶器中,动力作用在C点,阻力作用在瓶盖上(可以看作作用在B点附近),由于动力臂(从A点到C点的距离)大于阻力臂(从A点到瓶盖边缘的距离),因此起瓶器是省力杠杆。
最后,我们确定在C点施加力的方向。由于起瓶器是省力杠杆,且动力臂大于阻力臂,根据杠杆原理,我们知道在动力臂上施加的力应该使杠杆绕着支点逆时针转动,从而打开瓶盖。因此,在C点应该施加一个向上的力。
【答案】:省力;A;向上。
7.(云南中考)如图所示,美丽乡村建设的工地上,工人使用一个
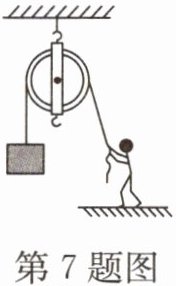
定
(填“定”或“动”)滑轮匀速提升重300N的建筑材料(不计绳重和摩擦),则人的拉力为300
N。
答案:
【解析】:
本题考查定滑轮的特点,定滑轮是轴的位置固定不动的滑轮,使用定滑轮时不能省力,但可以改变力的方向,已知建筑材料重$300N$,不计绳重和摩擦,根据定滑轮的特点,人的拉力$F$等于建筑材料的重力$G$,即$F = G=300N$。
【答案】:
定;$300$
本题考查定滑轮的特点,定滑轮是轴的位置固定不动的滑轮,使用定滑轮时不能省力,但可以改变力的方向,已知建筑材料重$300N$,不计绳重和摩擦,根据定滑轮的特点,人的拉力$F$等于建筑材料的重力$G$,即$F = G=300N$。
【答案】:
定;$300$
8.(常州中考)如图所示,工人利用动滑轮匀速提升重物,已知物重400N,施加在绳端竖直向上的拉力F为250N,在100s内将物体提升10m。不计绳重与摩擦,此过程中动滑轮的机械效率为
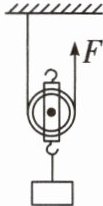
80%
,绳端拉力做功的功率为50
W。
答案:
【解析】:
本题主要考查动滑轮机械效率和拉力做功功率的计算。
对于动滑轮机械效率的计算,需要用到公式$\\eta = \frac{W_{有}}{W_{总}}\× 100\\%$,其中$W_{有}$是有用功,即提升重物所做的功,$W_{总}$是总功,即拉力所做的功。
首先计算有用功,根据公式$W_{有} = Gh$,其中$G$是物重,$h$是物体上升的高度。
然后计算总功,由于使用动滑轮,绳子自由端移动的距离$s$是物体上升高度$h$的两倍,即$s = 2h$,再根据公式$W_{总} = Fs$计算总功。
最后,将有用功和总功代入机械效率公式计算即可。
对于拉力做功的功率,需要用到公式$P = \frac{W_{总}}{t}$,其中$W_{总}$是总功,$t$是时间。
根据上述分析,首先计算有用功:$W_{有} = Gh = 400 \× 10= 4000J$,
接着计算总功:由于使用动滑轮,$s = 2h = 2 \× 10 = 20m$,
所以$W_{总} = Fs = 250\× 20 = 5000J$,
然后计算机械效率:$\\eta = \frac{W_{有}}{W_{总}}\× 100\\% = \frac{4000}{5000} \× 100\\% = 80\\%$,
最后计算拉力做功的功率:$P = \frac{W_{总}}{t} = \frac{5000}{100} = 50W$。
【答案】:$80\\%$;$50$。
本题主要考查动滑轮机械效率和拉力做功功率的计算。
对于动滑轮机械效率的计算,需要用到公式$\\eta = \frac{W_{有}}{W_{总}}\× 100\\%$,其中$W_{有}$是有用功,即提升重物所做的功,$W_{总}$是总功,即拉力所做的功。
首先计算有用功,根据公式$W_{有} = Gh$,其中$G$是物重,$h$是物体上升的高度。
然后计算总功,由于使用动滑轮,绳子自由端移动的距离$s$是物体上升高度$h$的两倍,即$s = 2h$,再根据公式$W_{总} = Fs$计算总功。
最后,将有用功和总功代入机械效率公式计算即可。
对于拉力做功的功率,需要用到公式$P = \frac{W_{总}}{t}$,其中$W_{总}$是总功,$t$是时间。
根据上述分析,首先计算有用功:$W_{有} = Gh = 400 \× 10= 4000J$,
接着计算总功:由于使用动滑轮,$s = 2h = 2 \× 10 = 20m$,
所以$W_{总} = Fs = 250\× 20 = 5000J$,
然后计算机械效率:$\\eta = \frac{W_{有}}{W_{总}}\× 100\\% = \frac{4000}{5000} \× 100\\% = 80\\%$,
最后计算拉力做功的功率:$P = \frac{W_{总}}{t} = \frac{5000}{100} = 50W$。
【答案】:$80\\%$;$50$。
查看更多完整答案,请扫码查看


