《2025年一本暑假计算加应用题四年级数学北师大版》

5. (分组法巧算)用简便方法计算:0.1+0.2+0.3+0.4+…+3.8+3.9。(11★)

答案： $0.1 + 0.2 + 0.3 + 0.4 + \cdots + 3.8 + 3.9$
$= (0.1 + 3.9)×39÷2$
$= 78$

6. (错中求解)林林在计算一道小数加法题时,把其中一个加数 3.8 看成了 8.3,得到的结果是 24.1。正确的结果是多少? (13★)

答案： $24.1 - 8.3 + 3.8 = 19.6$
答：正确的结果是19.6。

7. (数三角形个数问题)下面图形中,一共有多少个三角形? (12★)

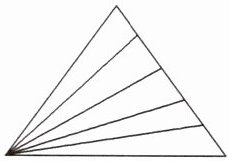
$5 + 4 + 3 + 2 + 1 = 15$（个）
答：一共有15个三角形。

答案： $5 + 4 + 3 + 2 + 1 = 15$（个）
答：一共有15个三角形。

8. (求等腰三角形内角度数)如图,在等腰三角形 ABC 内有一个等腰三角形 BCD,并且∠1= ∠2,∠3= ∠4,∠D= 120°,你能求出∠A 的度数吗? (13★)

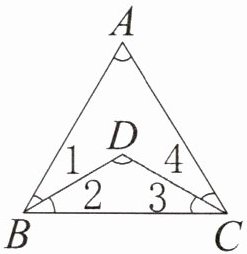
因为三角形BCD是等腰三角形，所以∠2 = ∠3。
因为∠1 = ∠2，∠3 = ∠4，所以∠1 = ∠2 = ∠3 = ∠4。
∠2 = (180° - ∠D)÷2 = (180° - 120°)÷2 = 30°
∠1 = ∠2 = ∠3 = ∠4 = 30°
∠A = 180° - ∠1 - ∠2 - ∠3 - ∠4 = 180° - 30° - 30° - 30° - 30° = 60°
答：∠A的度数为60°。

答案： 因为三角形BCD是等腰三角形，所以$\angle 2 = \angle 3$。
因为$\angle 1 = \angle 2$，$\angle 3 = \angle 4$，所以$\angle 1 = \angle 2 = \angle 3 = \angle 4$。
$\angle 2 = (180^{\circ} - \angle D)÷2 = (180^{\circ} - 120^{\circ})÷2 = 30^{\circ}$
$\angle 1 = \angle 2 = \angle 3 = \angle 4 = 30^{\circ}$
$\angle A = 180^{\circ} - \angle 1 - \angle 2 - \angle 3 - \angle 4 = 180^{\circ} - 30^{\circ} - 30^{\circ} - 30^{\circ} - 30^{\circ} = 60^{\circ}$
答：$\angle A$的度数为$60^{\circ}$。