《2025年亮点给力提优课时作业本六年级数学上册苏教版江苏专版》

例1(教材P9)下图表示用棱长1厘米的正方体摆成的物体。

(1)从前面、上面和右面看到的分别是什么形状?试着画一画。
(2)这个物体的表面积是多少平方厘米?
(3)如果添加同样的正方体,把这个物体补成一个大正方体,表面积至少是多少平方厘米?
思路分析(1)要画出从前面、上面和右面看到的形状,可以先数一数分别从某一面能看到几个正方形,再看一看这些正方形有几行,每一行是怎么排列的。(2)可以先算出一个正方形的面积,然后根据物体的前后、左右和上下的面积对应相同,利用(前面的面积+上面的面积+右面的面积)×2来计算它的表面积。(3)补成一个大正方体,要按照长、宽、高里面最长的来确定棱长,上下有三层,前后有三排,左右有三列,所以补成的大正方体的棱长至少是3厘米,进而算出大正方体的表面积。

答案：
(1)
从前面看：
□□□
□□□
□
从上面看：
□□□
□□
从右面看：
□□
□□
□
(2)
前面有$7$个面，上面有$6$个面，右面有$5$个面。
一个面面积为$1×1 = 1$平方厘米。
表面积为$(7 + 6 + 5)×2×1 = 36$平方厘米。
(3)
大正方体棱长至少是$3$厘米。
大正方体表面积为$3×3×6 = 54$平方厘米。

(2)$1×1×(7+7+6)×2= 40$(平方厘米)
答:这个物体的表面积是40平方厘米。
(3)补成的大正方体的棱长至少是3厘米。
$3×3×6= 54$(平方厘米)
答:表面积至少是54平方厘米。

答案：
(2)
物体前后左右上下6个面各有7、7、7、7、6、6平方厘米的面积。
$1 × 1 × (7 + 7 + 6) × 2 = 40 (平方厘米)$
答: 这个物体的表面积是40平方厘米。
(3)
补成大正方体后，棱长至少是3厘米。
$3 × 3 × 6 = 54 (平方厘米)$
答: 表面积至少是54平方厘米。

求不规则物体的表面积,可以先求部分面积,再根据物体的特点求出总面积。像这样由若干个相同的正方体摆成的物体,表面积一般用(上面的面积+前面的面积+右面的面积)×2来计算。

答案： 答题卡：
解：
对于由若干个相同的正方体摆成的物体，其表面积计算方法如下：
1. 确定上面的面积、前面的面积和右面的面积。
2. 将上述三个面的面积相加，然后乘以2，即得到物体的总表面积。
公式表示为：总表面积 = (上面的面积 + 前面的面积 + 右面的面积) × 2。

跟踪练习1新素养几何直观用16个棱长为2厘米的小正方体摆成如下图的物体。

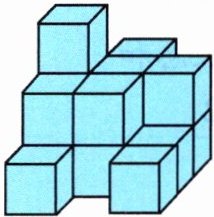
(1)从前面、上面和右面看到的分别是什么形状?试着画一画。
(2)这个物体的表面积是( )平方厘米。
(3)至少添加( )个同样的小正方体可以把这个物体补成一个大正方体,这个大正方体的表面积是( )平方厘米。

答案：

(1)
(2)200
(3)48 384

例2(教材P15)你能根据正方体的体积来估计右边物体的体积吗?

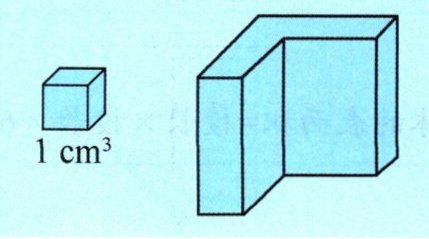
思路分析要想知道右边物体的体积,就要估一估右边的物体里面含有几个体积是$1cm^{3}$的正方体。图中右边的物体是一个不规则图形,我们可以根据图中左边的正方体的大小把右边的物体进行分割(如下图),就能知道该物体中大约含有几个体积是$1cm^{3}$的正方体。

规范解答右边物体的体积大约是$15cm^{3}$。

答案： 将右边不规则物体进行分割，可看作由 15 个体积是$1cm^{3}$的小正方体组成，所以右边物体的体积大约是$15cm^{3}$。