《2025年亮点给力提优课时作业本六年级数学上册苏教版江苏专版》

先确定1份的量,再分别找出要求的比的未知量和1份的量之间的数量关系,就能顺利地借由1份的量求出未知量之间的比,从而解决问题。

答案： 假设题目：甲、乙两人的速度比是$ 4:3$，两人同时从A、B两地相向而行，20分钟后相遇。相遇后继续前进，问甲到达B地时，乙离A地还有600米。求A、B两地的距离。
设A、B两地的距离为$s$米，甲的速度为$4x$米/分钟，乙的速度为$3x$米/分钟。
根据题意，两人20分钟后相遇，可得：
$20 × (4x + 3x) = s$
即：
$20 × 7x = s$
$s = 140x$
甲走完全程所需时间为：
$\frac{s}{4x} = \frac{140x}{4x} = 35 分钟$
乙在35分钟内走的距离为：
$35 × 3x = 105x$
乙离A地还有的距离为：
$s - 105x = 140x - 105x = 35x$
由题意知，这个距离是600米，所以：
$35x = 600$
$x = \frac{600}{35} = \frac{120}{7}$
将$x$的值代入$s = 140x$，得到：
$s = 140 × \frac{120}{7} = 2400 米 = 2.4 千米$
答：A、B两地的距离是2.4千米。

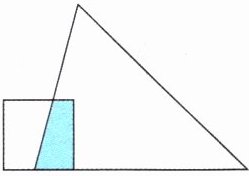
跟踪练习2 新素养 几何直观 如图,涂色部分的面积相当于正方形面积的$$ \frac { 2 } { 5 } $$,相当于三角形面积的$$ \frac { 1 } { 10 } $$,三角形与正方形的面积的比是多少？如果涂色部分的面积是8平方厘米,那么这组图形的总面积是多少？

答案： 正方形面积×$\frac{2}{5}$=三角形面积×$\frac{1}{10}$ 三角形面积:正方形面积=10:$\frac{5}{2}$=4:1 总面积:8÷$\frac{2}{5}$+8÷$\frac{1}{10}$−8=92(平方厘米)

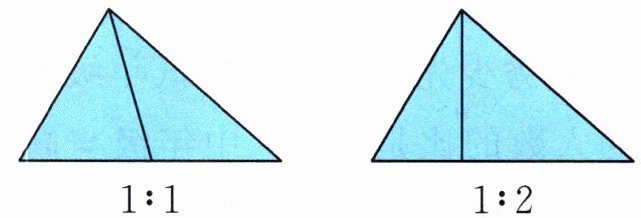
例3(教材P62)把下面的三角形分成两部分,使这两部分面积的比是$$ 1 : 1 $$,你能分一分吗？如果要使两部分面积的比是$$ 1 : 2 $$,又该怎样分？

思路分析 根据三角形面积公式和比的基本性质可知,如果两个三角形的高相等,那么它们的底的比与面积的比相等。
|两部分面积的比|$$ 1 : 1 $$|$$ 1 : 2 $$|
|底边长度分割的比|$$ 1 : 1 $$|$$ 1 : 2 $$|
规范解答 答案不唯一,如：

答案： 1. 当两部分面积的比是$1:1$时：
从三角形顶点向底边作中线（连接顶点与底边中点），将三角形分成两个小三角形，这两个小三角形等底等高，根据三角形面积公式$S = \frac{1}{2}ah$（$a$为底，$h$为高），它们面积相等，面积比为$1:1$，底边长度分割比也为$1:1$。
2. 当两部分面积的比是$1:2$时：
把底边分成$1:2$的两段，设底边总长度为$3x$，一段为$x$，另一段为$2x$，然后从顶点分别连接底边这两个分点，得到两个小三角形，这两个小三角形高相等，根据三角形面积公式，它们面积比等于底边长度比，即为$1:2$。
综上，面积比为$1:1$时，作底边中线；面积比为$1:2$时，把底边按$1:2$分割后连接顶点与分点。

高相等时,三角形面积的比就是底的比,可以运用这个规律分割图形。

答案： 设两个三角形的高都是$h$，第一个三角形的底为$a$，第二个三角形的底为$b$。
第一个三角形的面积：
$S_1 = \frac{1}{2} × a × h$。
第二个三角形的面积：
$S_2 = \frac{1}{2} × b × h$。
面积比：
$\frac{S_1}{S_2} = \frac{\frac{1}{2} × a × h}{\frac{1}{2} × b × h} = \frac{a}{b}$。
结论：
当两个三角形的高相等时，它们的面积之比等于它们的底之比。

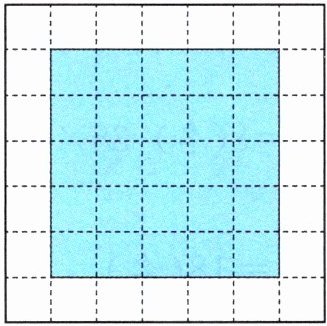
跟踪练习3 如图的每个小方格都是$$ 1 × 1 $$的正方形,请把图中涂色部分的正方形分成一个直角三角形和一个直角梯形,使它们的面积的比是$$ 2 : 3 $$。

答案：
画法不唯一，如:

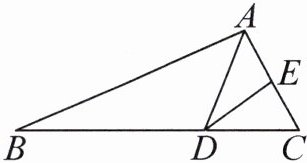
跟踪练习4 如图,在三角形ABC中,$$ B C = 3 D C $$,$$ A E = E C $$,三角形ADE的面积是2.5平方厘米,则三角形ABC的面积是多少平方厘米？

答案： 2.5×2×3=15(平方厘米)
解析：高相等时，三角形面积的比就是底的比。因为AE=EC，所以三角形ADE的面积与三角形DEC的面积相等，即$S_{三角形ADC}$=2.5×2=5(平方厘米)；因为BC=3DC，所以三角形ABC的面积是三角形ADC面积的3倍，即$S_{三角形ABC}$=5×3=15(平方厘米)。