《2025年假期向前冲暑假作业八年级物理人教版》

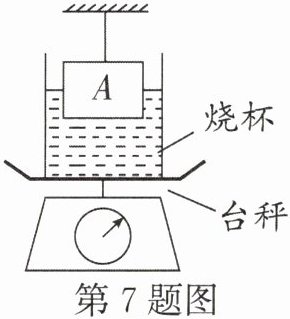
7. 如图所示,台秤上放置一个装有适量水的烧杯,已知烧杯和水的总质量为400g,杯的底面积为$100cm^2,$将一个质量为300g、体积为$200cm^3$的长方体实心物体A用细线吊着,然后将其一半浸入烧杯的水中(烧杯的厚度忽略不计,杯内水没有溢出,g取10N/kg)。则:
(1)物体A的密度是$______g/cm^3,$当物体A的一半浸入水中后,如图,水对烧杯底部的压强增大了______Pa。
(2)物体A所受的浮力为______N,细线对物体A的拉力为______N,台秤的示数为______N,此时烧杯对台秤的压强为______Pa。

答案：
(1)1.5 100
(2)1 2 5 500 解析:
(1)物体A的密度:
$ρ=\frac {m}{V}=\frac {300g}{200cm^{3}}=1.5g/cm^{3}$;物体A的一半浸入水中时受到的浮力:$F_{浮}=ρ_{水}gV_{排}=1.0×10^{3}kg/m^{3}×10N/kg×\frac {1}{2}×$
$200×10^{-6}m^{3}=1N$;由于力的作用是相互的,水对物体A有向上的浮力,物体A对水有向下的压力,所以水对烧杯底部增大的压力:$ΔF=F_{浮}=1N$,所以水对烧杯底部增大的压强:
$Δp=\frac {ΔF}{S}=\frac {1N}{100×10^{-4}m^{2}}=100Pa$。
(2)物体A的重力:
$G_{A}=m_{A}g=0.3kg×10N/kg=3N$,细线对物体A的拉力:
$F_{拉}=G_{A}-F_{浮}=3N-1N=2N$,台秤的示数即台秤受到的压力,则台秤的示数等于烧杯和水的重力、物体A对水向下的作用力之和,台秤的示数:$F=G_{杯和水}+F_{浮}=0.4kg×10N/kg+$
$1N=5N$,烧杯对台秤的压强:$p=\frac {F}{S}=\frac {5N}{100×10^{-4}m^{2}}=$
500 Pa。

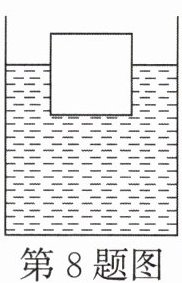
8. 如图所示,盛有2kg水的柱形容器置于水平地面上,重为6N不吸水的正方体,静止时有五分之三的体积浸入水中,物体下表面与水面平行,则物体的密度为$______kg/m^3,$物体下表面所受水的压力为______N。若物体在压力的作用下刚好浸没水中,不接触容器底,水不溢出,此时水对容器底部的压力为______N。(g取10N/kg,ρ水$= 1.0×10^3kg/m^3)$

答案： $0.6×10^{3}$ 6 30 解析:由图可知,物体在水中处于漂浮状态,则物体所受的浮力为$F_{浮}=G=6N$,假设物体的体积为V,根据阿基米德原理可知$ρ_{水}g\frac {3}{5}V=F_{浮}=6N$,解得$V=$
$\frac {F_{浮}}{\frac {3}{5}ρ_{水}g}=\frac {6N}{\frac {3}{5}×1.0×10^{3}kg/m^{3}×10N/kg}=1×10^{-3}m^{3}$;物体的质量为$m=\frac {G}{g}=\frac {6N}{10N/kg}=0.6kg$,则物体的密度为$ρ=\frac {m}{V}=$
$\frac {0.6kg}{1×10^{-3}m^{3}}=0.6×10^{3}kg/m^{3}$。根据浮力产生的原因$F_{浮}=$
$F_{向上}-F_{向下}$,物体上表面没有受到水的压力,则物体下表面所受水的压力为$F=F_{向上}=F_{浮}=6N$,物体在压力的作用下刚好浸没水中静止时,物体受到向上的浮力$F'_{浮}$和向下的重力G及向下的压力$F'$,则物体此时受的浮力$F'_{浮}=$
$ρ_{水}gV_{排}=1.0×10^{3}kg/m^{3}×10N/kg×1×10^{-3}m^{3}=10N$,力的作用是相互的,水给物体的浮力为10N,则物体给水的压力也为10N,容器中水的重力$G_{水}=m_{水}g=2kg×10N/kg=$
20N,此时水对容器底部的压力为$F_{压}=F'_{浮}+G_{水}=10N+$
$20N=30N$。

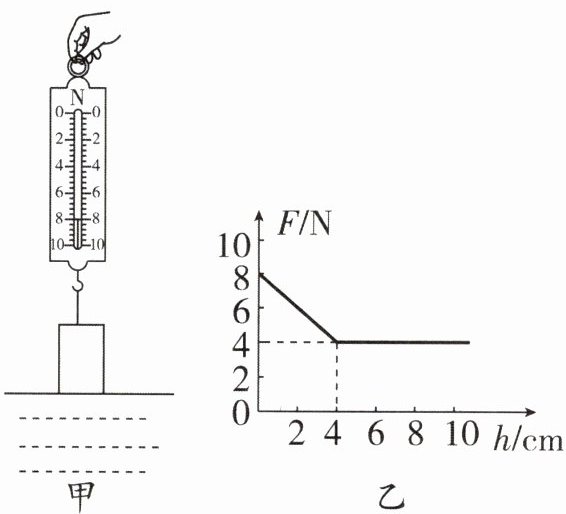
9. 用弹簧测力计悬挂一实心物块,物块下表面与水面刚好接触,如图甲所示。从此处匀速下放物块,直至浸没于水中并继续匀速下放(物块未与水底接触)。物块下放过程中,弹簧测力计示数F与物块下表面浸入水的深度h的关系如图乙。g取10N/kg,水的密度是$1.0×10^3kg/m^3。$求:
(1)物块完全浸没在水中受到的浮力是多少?
(2)物块刚好完全浸没时下表面受到水的压强是多少?
(3)物块的密度是多少?

答案： 解:
(1)由图像可知,当$h=0$时(物块没有浸入水中),弹簧测力计的示数$F_{拉1}=8N$,则物块的重力:$G=F_{拉1}=8N;$
当物块完全浸没在水中时,弹簧测力计的示数$F_{拉2}=4N$,则物块完全浸没在水中时受到的浮力:
$F_{浮}=G-F_{拉2}=8N-4N=4N$。
(2)由图像可知,物块刚浸没时下表面所处的深度:
$h=4cm=0.04m,$
则物块刚好完全浸没时下表面受到水的压强:
$p=ρ_{水}gh=1.0×10^{3}kg/m^{3}×10N/kg×0.04m=400Pa$。
(3)物块的质量:$m=\frac {G}{g}=\frac {8N}{10N/kg}=0.8kg,$
由$F_{浮}=ρ_{水}gV_{排}$可得物块的体积:
$V=V_{排}=\frac {F_{浮}}{ρ_{水}g}=\frac {4N}{1.0×10^{3}kg/m^{3}×10N/kg}=4×10^{-4}m^{3},$
则物块的密度:$ρ_{物}=\frac {m}{V}=\frac {0.8kg}{4×10^{-4}m^{3}}=2×10^{3}kg/m^{3}$。