《2025年全品学练考九年级数学上册沪科版》

课堂检测
1. 如图22-4-8，若$\triangle ABC\backsim\triangle DEF$，则$\triangle ABC$与$\triangle DEF$是以点 O为位似中心的位似图形. 若$\frac {OA}{OD}=\frac {2}{3}$，则$\triangle ABC$与$\triangle DEF$的相似比是$\frac {2}{3}$.

答案： 点 O $\frac {2}{3}$

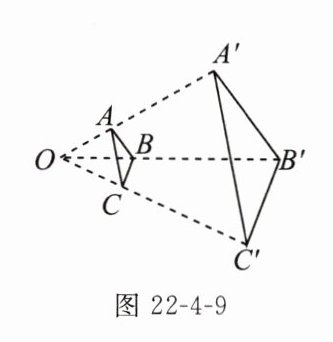
2. (2023长春)如图22-4-9，$\triangle ABC$和$\triangle A'B'C'$是以点O为位似中心的位似图形，点A在线段$OA'$上. 若$OA:AA'=1:2$，则$\triangle ABC$与$\triangle A'B'C'$的周长之比为____$\frac {1}{3}$.

答案： $\frac {1}{3}$

3. 在如图22-4-10所示的正方形网格中，$\triangle ABC$的顶点均在网格的格点上，以图中的点O为位似中心，将$\triangle ABC$放大为原来的2倍.
按照以下步骤画出$\triangle A'B'C'$：1. 连接$OA$、$OB$、$OC$并延长。延长$OA$到$A'$，使$OA' = 2OA$；延长$OB$到$B'$，使$OB' = 2OB$；延长$OC$到$C'$，使$OC' = 2OC$。2. 连接$A'B'$、$B'C'$、$C'A'$，则$\triangle A'B'C'$就是所求图形（具体图形根据网格实际操作绘制）。

答案： 【解析】：
1. 连接$OA$、$OB$、$OC$并延长。
延长$OA$到$A'$，使$OA' = 2OA$；延长$OB$到$B'$，使$OB' = 2OB$；延长$OC$到$C'$，使$OC' = 2OC$。
2. 连接$A'B'$、$B'C'$、$C'A'$，则$\triangle A'B'C'$就是以点$O$为位似中心，将$\triangle ABC$放大为原来$2$倍后的图形。
【答案】：按照上述步骤画出$\triangle A'B'C'$（具体图形根据网格实际操作绘制）。

例 (教材补充例题)如图22-4-11，在平面直角坐标系中，有两点A(6,3)，B(6,0)。以原点O为位似中心，把线段AB缩小为原来的$\frac{1}{3}，$求出各对应点的坐标并观察对应点之间坐标的变化，你有什么发现？

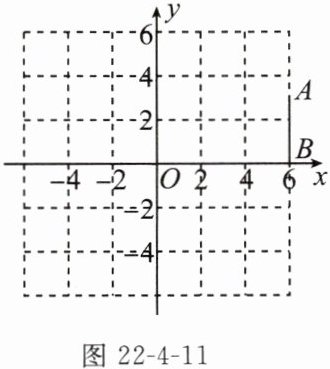
当位似图形在位似中心O同侧时，A，B的对应点坐标分别为(2,1)，(2,0)；当位似图形在位似中心O两侧时，A，B的对应点坐标分别为(-2,-1)，(-2,0)。发现：在平面直角坐标系中，如果以原点为位似中心，画出一个与原图形位似的图形，使它与原图形的相似比为k，那么与原图形上的点(x,y)对应的位似图形上的点的坐标为(kx,ky)或(-kx,-ky)。

答案： 【解析】：
- 当位似图形在位似中心$O$的同侧时：
已知$A(6,3)$，$B(6,0)$，以原点$O$为位似中心，把线段$AB$缩小为原来的$\frac{1}{3}$。
根据位似变换的性质，若位似比为$k = \frac{1}{3}$，且在位似中心同侧，则对应点坐标的比等于$k$。
对于点$A(6,3)$，其对应点$A_1$的横坐标为$6×\frac{1}{3}=2$，纵坐标为$3×\frac{1}{3}=1$，即$A_1(2,1)$；
对于点$B(6,0)$，其对应点$B_1$的横坐标为$6×\frac{1}{3}=2$，纵坐标为$0×\frac{1}{3}=0$，即$B_1(2,0)$。
当位似图形在位似中心$O$的两侧时：
此时位似比$k=-\frac{1}{3}$。
对于点$A(6,3)$，其对应点$A_2$的横坐标为$6×(-\frac{1}{3})=-2$，纵坐标为$3×(-\frac{1}{3})=-1$，即$A_2(-2,-1)$；
对于点$B(6,0)$，其对应点$B_2$的横坐标为$6×(-\frac{1}{3})=-2$，纵坐标为$0×(-\frac{1}{3}) = 0$，即$B_2(-2,0)$。
发现：在平面直角坐标系中，如果以原点为位似中心，画出一个与原图形位似的图形，使它与原图形的相似比为$k$，那么与原图形上的点$(x,y)$对应的位似图形上的点的坐标为$(kx,ky)$或$(-kx,-ky)$。
【答案】：
当位似图形在位似中心$O$同侧时，$A$，$B$的对应点坐标分别为$(2,1)$，$(2,0)$；当位似图形在位似中心$O$两侧时，$A$，$B$的对应点坐标分别为$(-2,-1)$，$(-2,0)$。发现：在平面直角坐标系中，如果以原点为位似中心，画出一个与原图形位似的图形，使它与原图形的相似比为$k$，那么与原图形上的点$(x,y)$对应的位似图形上的点的坐标为$(kx,ky)$或$(-kx,-ky)$。

变式1 在平面直角坐标系中，已知点E(-4,2)，F(-2,-2)，以原点O为位似中心，把△EFO缩小为原来的$\frac{1}{2}，$则点E的对应点的坐标是（D）
A. (2,-1)
B. (-8,4)
C. (-8,4)或(8,-4)
D. (-2,1)或(2,-1)

答案： 变式 1 D