《2025年全品学练考九年级数学上册沪科版》

例1 (教材补充例题)在同一平面直角坐标系中画出反比例函数$y=\frac{3}{x}$和$y=-\frac{3}{x}$的图象,并解决下列问题:
(1)填写下面的表格:

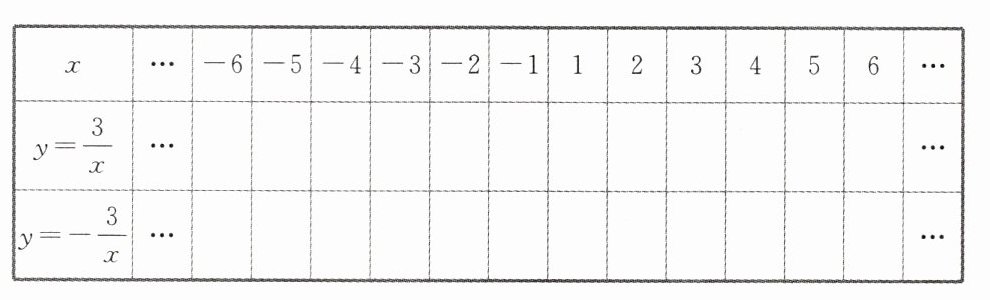
(2)分别在图21-5-3①②中画出反比例函数$y=\frac{3}{x}$和$y=-\frac{3}{x}$的图象.

(3)观察上述函数的图象,可知反比例函数图象的形状是双曲线;因为自变量x与函数y的值都不能取0,故反比例函数的图象与x轴,y轴都无交点.
(4)若点$(a,b)$在反比例函数$y=\frac{3}{x}$的图象上,则点$(-a,-b)$在反比例函数$y=\frac{3}{x}$的图象上;点$(a,-b)$和$(-a,b)$在反比例函数$y=-\frac{3}{x}$的图象上.

答案：
(1)略
(2)略
(3)双曲线 0 无
(4)在 在

变式 画出函数$y=\frac{6}{x}$和$y=-\frac{6}{x}$的图象.
函数$y = \frac{6}{x}$的图象是位于第一、三象限的双曲线，函数$y=-\frac{6}{x}$的图象是位于第二、四象限的双曲线。（具体图象需通过在平面直角坐标系中按上述描点法准确绘制得出）

答案： 【解析】：
1. 首先明确反比例函数的图象是双曲线，对于反比例函数$y = \frac{k}{x}(k\neq0)$，当$k＞0$时，图象在一、三象限；当$k ＜ 0$时，图象在二、四象限。
对于函数$y=\frac{6}{x}$，其中$k = 6＞0$，所以它的图象在第一、三象限；对于函数$y=-\frac{6}{x}$，其中$k=-6 ＜ 0$，所以它的图象在第二、四象限。
2. 然后用描点法来画函数图象：
对于函数$y = \frac{6}{x}$：
列表：选取一些$x$的值，计算出对应的$y$值。
当$x = 1$时，$y=\frac{6}{1}=6$；当$x = 2$时，$y=\frac{6}{2}=3$；当$x = 3$时，$y=\frac{6}{3}=2$；当$x=-1$时，$y=\frac{6}{-1}=-6$；当$x=-2$时，$y=\frac{6}{-2}=-3$；当$x=-3$时，$y=\frac{6}{-3}=-2$。
描点：在平面直角坐标系中，根据列表中的坐标$(1,6)$，$(2,3)$，$(3,2)$，$( - 1,-6)$，$( - 2,-3)$，$( - 3,-2)$等描出相应的点。
连线：用平滑的曲线将第一象限内的点依次连接起来，得到图象在第一象限的部分；用平滑的曲线将第三象限内的点依次连接起来，得到图象在第三象限的部分。
对于函数$y=-\frac{6}{x}$：
列表：同样选取一些$x$的值，计算对应的$y$值。
当$x = 1$时，$y=-\frac{6}{1}=-6$；当$x = 2$时，$y=-\frac{6}{2}=-3$；当$x = 3$时，$y=-\frac{6}{3}=-2$；当$x=-1$时，$y=-\frac{6}{-1}=6$；当$x=-2$时，$y=-\frac{6}{-2}=3$；当$x=-3$时，$y=-\frac{6}{-3}=2$。
描点：在平面直角坐标系中，根据列表中的坐标$(1,-6)$，$(2,-3)$，$(3,-2)$，$( - 1,6)$，$( - 2,3)$，$( - 3,2)$等描出相应的点。
连线：用平滑的曲线将第二象限内的点依次连接起来，得到图象在第二象限的部分；用平滑的曲线将第四象限内的点依次连接起来，得到图象在第四象限的部分。
【答案】：函数$y = \frac{6}{x}$的图象是位于第一、三象限的双曲线，函数$y=-\frac{6}{x}$的图象是位于第二、四象限的双曲线。（具体图象需通过在平面直角坐标系中按上述描点法准确绘制得出）

观察思考
观察反比例函数$y=\frac{6}{x}$和$y=-\frac{6}{x}$的图象,思考下列问题:
(1)反比例函数的图象是什么形状?其位置与比例系数k有什么关系?
答：反比例函数的图象是双曲线。当$k＞0$时,图象的两支分别位于第一、三象限;当$k＜0$时,图象的两支分别位于第二、四象限。
(2)在每个象限内,函数y随x的增大是怎样变化的?
答：对于函数$y=\frac{6}{x}$的图象,在每个象限内,函数y随x的增大而减小;对于函数$y=-\frac{6}{x}$的图象,在每个象限内,函数y随x的增大而增大。

答案： 解:
(1)反比例函数的图象是双曲线.当$k＞0$时,图象的两支分别位于第一、三象限;当$k＜0$时,图象的两支分别位于第二、四象限.
(2)对于函数$y=\frac{6}{x}$的图象,在每个象限内,函数y随x的增大而减小;对于函数$y=-\frac{6}{x}$的图象,在每个象限内,函数y随x的增大而增大.