《2024年新疆名校单元检测试卷九年级数学全一册人教版》

8. 如图，△ABC是一块绿化带，将阴影部分修建为花圃，已知AB = 15，AC = 9，BC = 12，阴影部分是△ABC的内切圆，一只自由飞翔的小鸟将随机落在这块绿化带上，则小鸟落在花圃上的概率为 （ ）
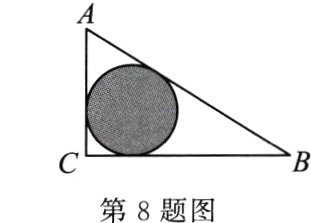
A. $\frac{1}{6}$ B. $\frac{\pi}{6}$ C. $\frac{\pi}{8}$ D. $\frac{\pi}{5}$
　　　　　　　　　　　

答案： B

9. 已知四个点的坐标分别是(-1，1)，(2，2)，$(\frac{2}{3}，\frac{3}{2})$，$(-5，\frac{1}{5})$，从中随机选取一个点，在反比例函数$y = \frac{1}{x}$图象上的概率是______.

答案： $\frac{1}{4}$

10. 如图，一只蚂蚁从点A出发到点D，E，F处寻觅食物. 假定蚂蚁在每个岔路口都可能随机选择一条向左下或右下的路径（比如A岔路口可以向左下到达B处，也可以向右下到达C处，其中A，B，C都是岔路口）. 那么，蚂蚁从A出发到达E处的概率是______.
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

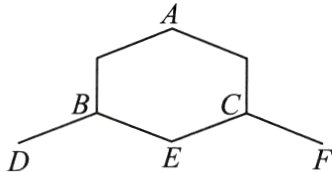
答案： $\frac{1}{2}$

11. 现有50张大小、质地及背面图案均相同的《西游记》任务卡片，正面朝下放置在桌面上，从中随机抽取一张并记下卡片正面所绘人物的名字后原样放回，洗匀后再抽. 通过多次试验后，发现抽到绘有孙悟空这个人物卡片的频率约为0.3. 估计这些卡片中绘有孙悟空这个人物的卡片张数约为______.

答案： 15

12. 荆楚学校为了了解九年级学生“一分钟内跳绳次数”的情况，随机选取了3名女生和2名男生，则从这5名学生中，选取2名同时跳绳，恰好选中一男一女的概率是______.

答案： $\frac{3}{5}$

13. 现有四张正面分别标有数字-1，1，2，3的不透明卡片，它们除数字外其余完全相同，将它们背面朝上洗均匀，随机抽取一张，记下数字后放回，背面朝上洗均匀，再随机抽取一张记下数字，前后两次抽取的数字分别记为m，n，则点P(m，n)在第二象限的概率为______.

答案：
$\frac{3}{16}$ [解析]画树状图如下：

一共有16种等可能的结果，其中点P(m,n)在第二象限的结果有(-1,1)，(-1,2)，(-1,3)，共3种，
∴P(点P在第二象限)=$\frac{3}{16}$.
故答案为：$\frac{3}{16}$.

14. 从-1，1，2这三个数字中，随机抽取一个数记为a，那么，使关于x的一次函数y = 2x + a的图象与x轴、y轴围成的三角形的面积为$\frac{1}{4}$，且使关于x的不等式组$\begin{cases}x + 2\leq a \\ 1 - x\leq 2a\end{cases}$有解的概率为______.

答案： $\frac{1}{3}$

15. (12分)有甲、乙两个不透明的布袋，甲袋中有　2个完全相同的小球，分别标有数字0和-2;乙袋中有3个完全相同的小球，分别标有数字-2，0和1，小明从甲袋中随机取出1个小球，记录标有的数字为x，再从乙袋中随机取出1个小球，记录标有的数字为y，这样确定了点Q的坐标(x，y).
(1)写出点Q所有可能的坐标;
(2)求点Q在x轴上的概率.

答案：
解：
(1)画树状图如下：

共有6种等可能的结果，点Q的坐标为(0，-2)，(0，0)，(0，1)，(-2，-2)，(-2，0)，(-2，1)；
(2)点Q在x轴上的情况有(0，0)，(-2，0)两种，所以点Q在x轴上的概率P=$\frac{2}{6}=\frac{1}{3}$.