《2024年新疆名校单元检测试卷九年级数学全一册人教版》

21. （7分）甲、乙两栋楼的位置如图所示,甲楼$AB$高16米. 当地中午12时,物高与影长的比是$1:\sqrt{2}$.
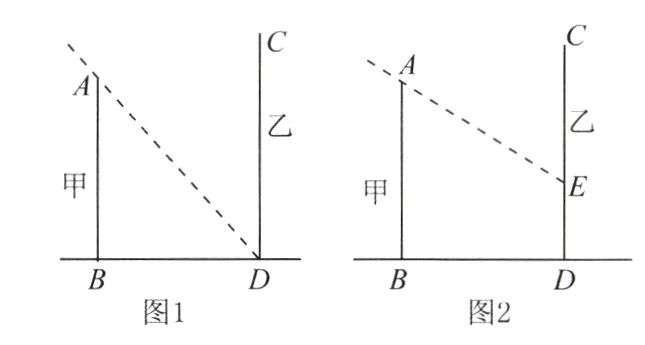
（1）如图1,当地中午12时,甲楼的影子刚好不落到乙楼上,则两楼间距$BD$的长为________米.
（2）当地下午14时,物高与影长的比是$1:2$. 如图2,甲楼的影子有一部分落在乙楼上,求落在乙楼上的影子$DE$的长.

答案：
解:
(1)16$\sqrt{2}$　[解析]由题意得
　　$\frac{AB}{BD}$ = $\frac{1}{\sqrt{2}}$，即$\frac{16}{BD}$ = $\frac{1}{\sqrt{2}}$，
　　解得BD = 16$\sqrt{2}$(米)，
　　故答案为:16$\sqrt{2}$;
(2)如图,作FE⊥AB于点F.在Rt△AEF中,∠AFE = 90°，EF = BD = 16$\sqrt{2}$米.
　　　　　　　　
　
∵物高与影长的比是1:2,
　
∴$\frac{AF}{EF}$ = $\frac{1}{2}$，
　
∴AF = $\frac{1}{2}$EF = 8$\sqrt{2}$(米)，
　故DE = FB = (16 - 8$\sqrt{2}$)米.
　答:落在乙楼上的影子DE的长为(16 - 8$\sqrt{2}$)米.

22. （8分）如图,李华晚上在路灯下散步. 已知李华的身高$AB = 1.8$米,灯柱的高$OP = O'P' = 18$米,两灯柱之间的距离$OO' = 30$米.
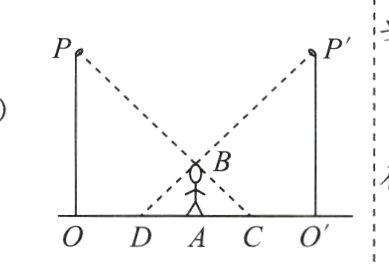
（1）若李华距灯柱$OP$的水平距离$OA = 18$米,求他影子$AC$的长;
（2）若李华在两路灯之间行走,则他前后的两个影子的长度之和($DA + AC$)是否是定值? 若为定值,求出该定值;若不是,请说明理由.

答案： 解:
(1)
∵AB//OP，
∴△ABC∽△OPC.
∴$\frac{AC}{OC}$ = $\frac{AB}{OP}$，
　
∵OP = 18，AB = 1.8，
∴$\frac{AC}{AC + 18}$ = $\frac{1.8}{18}$，
解得:AC = 2.
(2)是定值.
∵AB//OP，
∴△ABC∽△OPC，设AC = a，则OA = 9a，AO' = 30 - 9a ，
∵AB//O'P'，
∴△DAB∽△DO'P'，
∴$\frac{DA}{AO'}$ = $\frac{1.8}{18 - 1.8}$ = $\frac{1}{9}$，解得:DA = $\frac{10}{3}$ - a，
　
∴DA + AC = $\frac{10}{3}$是定值.

23. （9分）如图1是一种包装盒的表面展开图,将它围起来可得到一个几何体的模型.


（1）这个几何体模型的名称是________.
（2）如图2是根据$a$,$b$,$h$的取值画出的几何体的主视图和俯视图(图中实线表示的长方形),请在网格中画出该几何体的左视图.
（3）若$h = a + b$,且$a$,$b$满足$\frac{1}{4}a^{2}+b^{2}-a - 6b + 10 = 0$,求该几何体的表面积.

答案：
解:
(1)长方体　
(2)根据图1所标注的相关线段的长度和给出的视图画出长方体是长，宽，高分别为4，5，2的长方体，则左视图是长为5，宽为2的长方形，如图.
　　　　　　
(3)将给出的式子中10拆分成1 + 9，则所给式子写成两个完全平方式，($\frac{1}{2}$a - 1)² + (b - 3)² = 0，则，$\frac{1}{2}$a - 1 = 0，b - 3 = 0，
∴a = 2，b = 3，所以h = a + b = 2 + 3 = 5.所以此长方体的表面积为六个面的面积和:2(2×3 + 5×2 + 3×5)=62.