《2024年新疆名校单元检测试卷九年级数学全一册人教版》

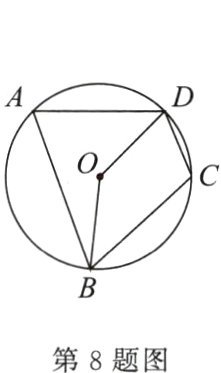
8. 如图,四边形ABCD是⊙O的内接四边形.若∠BCD = 121°,则∠BOD的度数为 （ ）
A. 138° B. 121° C. 118° D. 112°
　　　　　　　　　　　　

答案： C [解析]
∵四边形 ABCD 内接于圆 O,
∴∠A + ∠C = 180°.
∵∠BCD = 121°,
∴∠A = 59°.
∴∠BOD = 2∠A = 118°.
故选:C.

9. 如图,在平面直角坐标系中,⊙P的圆心是(2,a)(a ＞ 2),半径为2,函数y = x的图象被⊙P截得的弦AB的长为2$\sqrt{3}$,则a的值是 （ ）
A. 2$\sqrt{2}$ B. 2 + $\sqrt{2}$ C. 2$\sqrt{3}$ D. 2 + $\sqrt{3}$
　　　　　　　　

答案： B [解析]过 P 点作 PE⊥AB 于 E,过 P 点作 PC⊥x 轴于 C,交 AB 于 D,连接 PA.
∵PE⊥AB,AB = 2$\sqrt{3}$,半径为 2,
∴AE = $\frac{1}{2}$AB = $\sqrt{3}$,PA = 2,
根据勾股定理得:PE = $\sqrt{2² - (\sqrt{3})²}$ = 1,
∵点 A 在直线 y = x 上,
∴∠AOC = 45°,
∵∠DCO = 90°,
∴∠ODC = 45°,
∴△OCD 是等腰直角三角形,
∴OC = CD = 2,
∴∠PDE = ∠ODC = 45°,
∴∠DPE = ∠PDE = 45°,
∴DE = PE = 1,
∴PD = $\sqrt{2}$.
∵⊙P 的圆心是(2,a),
∴a = PD + DC = 2 + $\sqrt{2}$.
故选:B.

10. 已知A,B,C三点在⊙O上,且AB是⊙O内接正三角形的边长,AC是⊙O内接正方形的边长,则∠BAC的度数为 （ ）
A. 15°或105°
B. 75°或15°
C. 75°
D. 105°

答案：
B [解析]①如图 1,
∵AB 是⊙O 内接正三角形的边长,AC 是⊙O 内接正方形的边长,
∴∠AOB = 120°,∠AOC = 90°,
∴∠BOC = 360° - 120° - 90° = 150°,
∴∠BAC = $\frac{1}{2}$∠BOC = 75°;
②如图 2,同①得出∠BAC = 15°,
故选:B.

11. 如图,⊙O是△ABC的外接圆,∠OCB = 40°,则∠A的度数等于______.
　　

答案： 50°

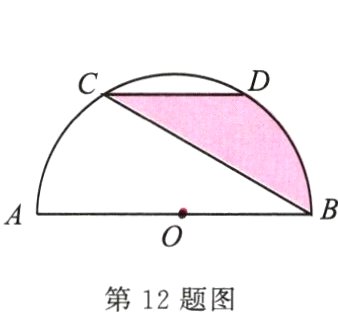
12. 如图,AB是半圆O的直径,点C,D是半圆O的三等分点,若弦CD = 2,则图中阴影部分的面积为______.
　　　

答案： $\frac{2π}{3}$

13. 已知扇形的圆心角为150°,它所对应的弧长20π cm,则此扇形的半径是______ cm,面积是______ cm².

答案： 24 240π

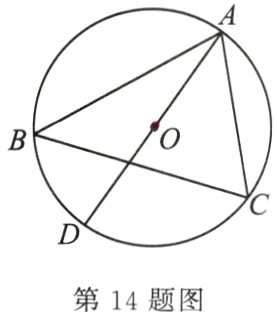
14. 如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC = 50°,则∠CAD =______.
　　　

答案： 40°

15. 若一个圆锥的侧面积是它底面积的2倍,则这个圆锥的侧面展开图的圆心角是______.

答案： 180° [解析]设底面圆的半径为 r,侧面展开扇形的半径为 R,扇形的圆心角为 n 度.由题意得 S底面面积 = πr²,
l底面周长 = 2πr,S扇形 = 2S底面面积 = 2πr²,l扇形弧长 = l底面周长 = 2πr.
由 S扇形 = $\frac{1}{2}$l扇形弧长×R 得 2πr² = $\frac{1}{2}$×2πr×R,
∴R = 2r.
由 l扇形弧长 = $\frac{nπR}{180}$,得 2πr = $\frac{nπ×2r}{180}$,解得 n = 180°.

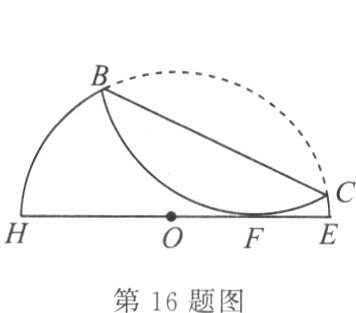
16. 如图,已知半圆O的直径HE = 4,沿它的一条弦折叠.若折叠后的圆弧与直径HE相切于点F,且HF:FE = 3:1,则折痕BC的长为______.
　　　

答案：
$\sqrt{11}$ [解析]如图,过 O 作弦 BC 的垂线 OP,垂足为 D,分别与弧的交点为 A,G,过切点 F 作 PF⊥半径 OE 交 OP 于点 P,

∵OP⊥BC,
∴BD = DC,即 OP 为 BC 的中垂线.
∴OP 必过弧 BGC 所在圆的圆心.
又
∵OE 为弧 BGC 所在圆的切线,PF⊥OE,
∴PF 必过弧 BGC 所在圆的圆心.
∴点 P 为弧 BGC 所在圆的圆心.
∵弧 BAC 沿 BC 折叠得到弧 BGC,
∴⊙P 为半径等于⊙O 的半径,即 PF = PG = OE = 2,且 AD = GD.
∴OG = AP.
∵F 点分⊙O 的直径为 3 : 1 两部分,
∴OF = 1.
在 Rt△OPF 中,设 OG = x,则 OP = x + 2,
∴OP² = OF² + PF²,即(x + 2)² = 1² + 2²,
解得 x = $\sqrt{5}$ - 2.
∴AG = 2 - ($\sqrt{5}$ - 2) = 4 - $\sqrt{5}$.
∴DG = $\frac{4 - \sqrt{5}}{2}$.
∴OD = OG + DG = $\sqrt{5}$ - 2 + $\frac{4 - \sqrt{5}}{2}$ = $\frac{\sqrt{5}}{2}$.
在 Rt△OBD 中,BD² = OB² - OD²,即 BD² = 2² - ($\frac{\sqrt{5}}{2}$)²,
∴BD = $\frac{\sqrt{11}}{2}$.
∴BC = 2BD = $\sqrt{11}$.

17. (6分)如图,矩形ABCD的边AB = 3 cm,BC = 4 cm,以点A为圆心,4 cm为半径作⊙A,则点B,C,D与⊙A怎样的位置关系?
　　　　

答案：
解:连接 AC,
∵AB = 3 cm,BC = AD = 4 cm,
∴AC = 5 cm,
∵AB＜4,AD = 4,AC＞4,
∴点 B 在⊙A 内,点 D 在⊙A 上,点 C 在⊙A 外.