《2024年新疆名校单元检测试卷九年级数学全一册人教版》

8. 已知矩形的周长为36 m,矩形绕着它的一条边旋转形成一个圆柱,设矩形的一条边长为 $x$ m,圆柱的侧面积为 $y$ $m^{2}$, 则 $y$ 与 $x$ 的函数关系式为 （ ）
A. $y = -2\pi x^{2}+18\pi x$
B. $y = 2\pi x^{2}-18\pi x$
C. $y = -2\pi x^{2}+36\pi x$
D. $y = 2\pi x^{2}-36\pi x$

答案： C

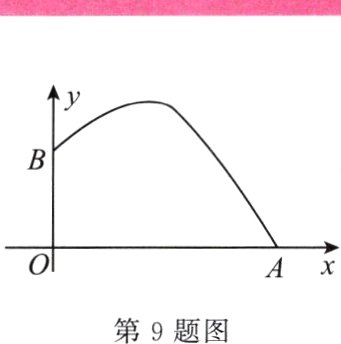
9. 在某次羽毛球混合团体锦标赛中,某次羽毛球的运动路线可以看作是抛物线 $y = -\frac{1}{4}x^{2}+bx + c$ 的一部分(如图),其中出球点 $B$ 离地面 $O$ 点的距离是1 m,球落地点 $A$ 到 $O$ 点的距离是4 m,那么这条抛物线的解析式是 （ ）
A. $y = -\frac{1}{4}x^{2}+\frac{3}{4}x + 1$ B. $y = -\frac{1}{4}x^{2}+\frac{3}{4}x - 1$
C. $y = -\frac{1}{4}x^{2}-\frac{3}{4}x + 1$ D. $y = -\frac{1}{4}x^{2}-\frac{3}{4}x - 1$
　　　　　　

答案： A [解析]
∵出球点$B$离地面$O$点的距离是$1\ m$，球落地点$A$到$O$点的距离是$4\ m$，
∴$B$点的坐标为$(0,1)$，$A$点坐标为$(4,0)$，
将两点代入解析式，得$\begin{cases}1 = c\\0=-4 + 4b + c\end{cases}$，
解得：$\begin{cases}b=\frac{3}{4}\\c = 1\end{cases}$，
∴这条抛物线的解析式是$y=-\frac{1}{4}x^{2}+\frac{3}{4}x + 1$.
故选：A.

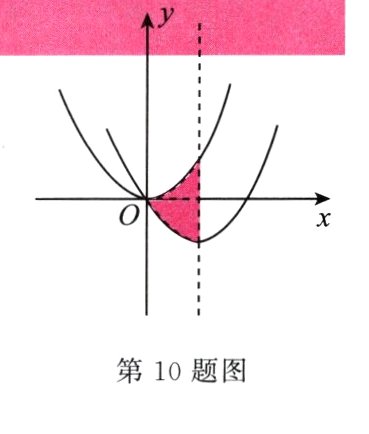
10. 如图,在平面直角坐标系中,抛物线 $y = \frac{1}{2}x^{2}$ 经过平移得到抛物线 $y = \frac{1}{2}x^{2}-2x$,其对称轴与两段抛物线所围成的阴影部分的面积为 （ ）
A. 2 B. 4
C. 8 D. 16
　　　　　　

答案：
B [解析]
∵$y=\frac{1}{2}x^{2}-2x=\frac{1}{2}(x - 2)^{2}-2$，
∴顶点坐标为$C(2,-2)$.
∴对称轴与两段抛物线所围成的阴影部分的面积为$2×2 = 4$.
故选B.

11. 在实验中我们常常采用利用计算机在平面直角坐标系中画出抛物线 $y = x^{2}$ 和直线 $y = -x + 3$,利用两图象交点的横坐标来求一元二次方程 $x^{2}+x - 3 = 0$ 的解,也可以在平面直角坐标系中画出抛物线 $y = x^{2}-3$ 和直线 $y = -x$,用它们交点的横坐标来求该方程的解. 所以求方程 $\frac{6}{x}-x^{2}+3 = 0$ 的近似解也可以利用熟悉的函数______和______的图象交点的横坐标来求得.

答案： $y=\frac{6}{x}$ $y=x^{2}-3$.

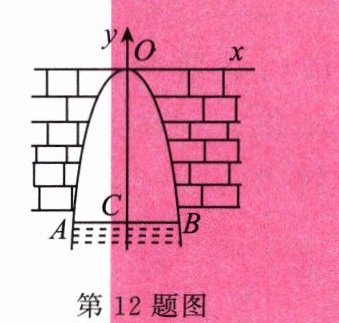
12. 如图,某涵洞的截面是抛物线形,现测得水面宽 $AB = 1.6$ m,涵洞顶点 $O$ 到水面的距离 $CO$ 为2.4 m,在图中直角坐标系内,涵洞截面所在抛物线的解析式是____________.

答案： $y=-\frac{15}{4}x^{2}$ [解析]设为$y=kx^{2}$，由$CO$和$AB$的长，得$A$的坐标为$(-0.8,-2.4)$，将其代入函数解析式得：
$-2.4=0.8×0.8×k$，解得$k=-\frac{15}{4}$.
∴函数的解析式为$y=-\frac{15}{4}x^{2}$.

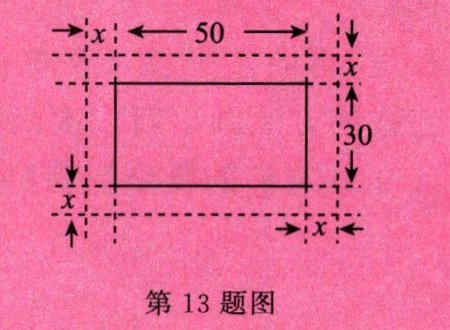
13. 如图,在一幅长50 cm,宽30 cm的矩形风景画的四周镶一条等宽的金色纸边,制成一幅矩形挂画,设整个挂画总面积为 $y$ $cm^{2}$,金色纸边的宽为 $x$ cm,则 $y$ 与 $x$ 的关系式是____________.
　　　　　　

答案： $y=4x^{2}+160x + 1500$

14. 二次函数 $y = x^{2}-2x + 1$ 在 $-5\leqslant x\leqslant3$ 范围内的最大值为______.

答案： 36 [解析]
∵$y=x^{2}-2x + 1=(x - 1)^{2}$，
∴抛物线开口向上，对称轴为直线$x=1$.
∴在$-5\leq x\leq3$的取值范围内，当$x=-5$时，有最大值$y=(-5 - 1)^{2}=36$，
故答案为36.

15. 如图,在同一坐标系中,作出① $y = 3x^{2}$② $y = \frac{1}{2}x^{2}$③ $y = x^{2}$ 的图象,则图象从里到外的三条抛物线对应的函数依次是____________.(填序号)
　　　　　　

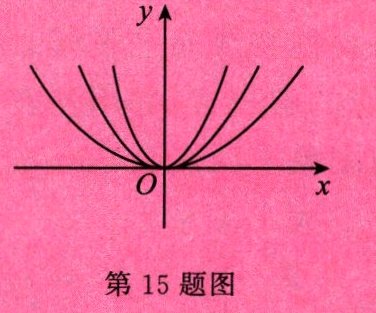
答案： ①③②

16. 已知二次函数 $y = x^{2}+4x + c$ 的图象与两坐标轴共有2个交点,则 $c =$______.

答案： 0或4 [解析]在二次函数$y=x^{2}+4x + c$中，当$x=0$时，$y=c$，函数与$y$轴一定有一个交点.
当二次函数经过原点时，$c=0$；
当二次函数不经过原点时，二次函数与$x$轴只有一个交点，则$b^{2}-4ac=16 - 4c=0$，
解得$c=4$.
故答案为：0或4.