《2025年亮点给力计算天天练六年级数学下册人教版》

1. 直接写出得数。
36%×100 = 　　　　　2.64 + 3.57 = 　　　　14.6 - 2.9 = 　　　　　3.14×4×25 = 　
86%÷43% = 　　　　72% + 28% = 　　　　3.14×0.1 = 　　　　　3.14×10²×4 = 　
2.4×0.3 = 　　　　　8.015×0 = 　　　　　2.25÷15 = 　　　　　28.26÷3.14÷3 = 　
30%÷$\frac{3}{10}$ = 　　　　　$\frac{2}{15}$÷$\frac{2}{7}$ = 　　　　　　　3.14×5 = 　　　　　　24×$\frac{1}{12}$ - $\frac{1}{5}$ = 　
3.14×9 = 　　　　　　3.14×30 = 　　　　　$\frac{7}{12}$×$\frac{3}{14}$ = 　　　　　　$\frac{3}{4}$×$\frac{5}{6}$÷$\frac{3}{4}$×$\frac{5}{6}$ = 　

答案： 36　　　　6.21　　　　11.7　　　　314 2　　　　　1　　　　　　0.314　　　1256
@@0.72　　　0　　　　　0.15　　　　3 1　　　　　$\frac{7}{15}$　　　　　15.7　　　　$1\frac{4}{5}$
@@28.26　　　94.2　　　　$\frac{1}{8}$　　　　　$\frac{25}{36}$

2. 计算下面各题，能简算的要简算。
$\frac{1}{2}$×101 - 50% 　　　　　260÷(50%÷$\frac{4}{5}$ + 1) 　　　　6.25×20×50%

答案： 50　　　　160　　　　62.5

3. 求下面各圆柱的体积。(单位$:dm)$
　　　　　　　　　
　　　　　　　　　　　　　　　　　　思维提升 补形法求体积

答案：
(1) $3.14×(6÷2)^2×10÷2 = 141.3(dm^3)$
(2) $50.24÷3.14÷2 = 8(dm)$
$3.14×8^2×10 = 2009.6(dm^3)$

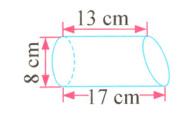
玻璃厂要加工一种艺术节奖杯(如下图)。加工时，一个有机玻璃圆柱正好可以截成两个这样的奖杯。求一个奖杯的体积。

答案：

$3.14×(8÷2)^2×(13 + 17)÷2 = 753.6(cm^3)$ 解析: 已知这个奖杯一端是斜面，所以不能通过圆柱的体积公式求得。将同样的两个奖杯拼补在一起(如图)，可以得到一个底面直径是8cm，高是(13 + 17)cm的圆柱，而所求奖杯的体积就是这个圆柱体积的一半。