《2025年周末小复习五年级数学下册人教版》

1. 容积的意义
箱子、油桶、仓库等所能容纳物体的________，通常叫作它们的容积。

答案： 体积

2. 容积单位
(1)计量容积，一般用体积单位。计量液体的体积，如水、油等，常用容积单位：________和________，用字母表示分别为________和________。1 L = ________mL。
(2)容积单位和体积单位的关系：1 L = ______dm³，1 mL = ______cm³。

答案：
(1)升 毫升 L mL 1000
(2)1 1

3. 容积的计算
(1)长方体或正方体容器容积的计算方法，跟体积的计算方法________，但要从容器________量长、宽、高。
(2)不规则物体体积的计算，一般把这些物体的体积转化为可测量、计算的液体的体积。

答案：
(1)相同 里面

二、（教材P38例5变式）一种酸奶采用长方体纸盒包装，从外面量，纸盒长6.4 cm、宽4 cm、高8.5 cm。盒子上标注着“净含量220 mL”，请问该标注是否真实？为什么？（8分）

答案： $6.4×4×8.5 = 217.6(cm^{3})$ $217.6\ cm^{3}=217.6\ mL$
$217.6＜220$
答：该标注不真实，因为标注的净含量比纸盒的体积大。

三、（教材$P41$练7变式）赵倩家有一个长方体玻璃鱼缸，长为8 $dm$，宽为4 $dm$，高为6 $dm$。鱼缸里原来有一些水（如图1），放入4个同样大小的装饰球后（如图2），水面上升了2 $cm$。平均每个装饰球的体积是多少立方厘米？（8分）

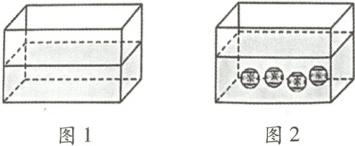
答案： $8\ dm = 80\ cm$ $4\ dm = 40\ cm$
$80×40×2÷4 = 1600(cm^{3})$
答：平均每个装饰球的体积是$1600\ cm^{3}$。