《2025年小学学霸作业本六年级数学下册青岛版山东专版》

三、操作题。
将下图的三角形以不同的直角边所在直线为轴旋转一周。

1. 画出你想到的两个立体图形。(在方框里面画草图，并标上相关数据)
2. 分别求出两个立体图形的体积。

答案：

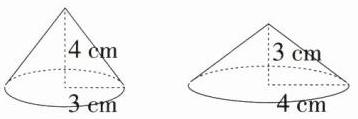
@@$3.14×3^{2}×4×\frac{1}{3}=37.68(cm^{3})$ $3.14×4^{2}×3×\frac{1}{3}=50.24(cm^{3})$

1. 随着人们需求的不断提高，一些“茶叶的衍生品”也随之丰富起来。茶香浓郁的茶冰淇淋深受人们喜爱。如图，有一个圆锥形茶冰淇淋，底面周长为$18.84\ cm$，高为$15.2\ cm$，它的体积是多少?

答案： $18.84÷3.14÷2 = 3(cm)$ $3.14×3^{2}×15.2×\frac{1}{3}=143.184(cm^{3})$

2. 奶茶已经逐渐成为年轻人生活中的一部分。有一个底面积是$78.5\ cm^{2}$、高是$15\ cm$的圆柱形奶茶杯，刚开始水面高度是$10\ cm$，然后在杯中完全浸入$8$个底面积是$3\ cm^{2}$、高是$2\ cm$的圆锥形水果块，杯里的水面高度现在是多少厘米?(结果保留一位小数)

答案： $3×2×\frac{1}{3}×8 = 16(cm^{3})$ $10 + 16÷78.5≈10.2(cm)$

3. 茶叶渣可以回收用来造纸。某品牌卷纸有两种包装，它们的纸质相同，规格及价格如图所示。
(1)制作图①中间的硬纸轴需要多少平方厘米的硬纸板?
(2)你觉得买哪一种更划算? 请通过计算说明。

答案：
(1)$3.14×4×10 = 125.6(cm^{2})$
(2)①$4÷2 = 2(cm)$ $\pi×(2 + 4)^{2}×10-\pi×2^{2}×10 = 320\pi(cm^{3})$ $320\pi÷3=\frac{320\pi}{3}(cm^{3})$ ②$4÷2 = 2(cm)$ $\pi×(2 + 8)^{2}×10-\pi×2^{2}×10 = 960\pi(cm^{3})$ $960\pi÷8 = 120\pi(cm^{3})$ $\frac{320\pi}{3}＜120\pi$，买第②种包装的更划算。