1. 感受一次函数 $y= 2x+1$ 的图像
(1)填表,并以表中各对 $x$、$y$ 的值为点的坐标,利用动态几何软件建立直角坐标系并构造这些点,如图 15-1.

| $x$ | …$$ | $-3.2$ | $-3$ | $-2.8$ | $-2.6$ | $-2$ | $-0.2$ | $0$ | $0.2$ | $0.4$ | $0.6$ | $0.8$ | $1$ | …$$ |

| $y= 2x+1$ | …$$ | ______ | ______ | ______ | ______ | ______ | ______ | ______ | ______ | ______ | ______ | ______ | ______ | …$$ |
(2)观察这些点,你有什么发现?
(3)再取更多的对应的 $x$、$y$ 值,并在直角坐标系中构造这些点,你有什么发现?
(4)猜想:一次函数 $y= 2x+1$ 的图像是什么图形?
(5)如图 15-2,打开动态几何软件,建立直角坐标系,在 $x$ 轴上构造一个点 $X$,记横坐标为 $x$,绘制动点 $P(x,2x+1)$;移动点 $X$,观察点 $P$ 经过的路径痕迹.你有什么发现?

(6)利用动态几何软件画函数 $y= -x+3$ 的图像.这个图像是什么样的图形?与你的猜想一致吗?
2. 探索一次函数 $y= kx+b$ 图像的性质
(1)打开动态几何软件,建立直角坐标系.如图 15-3,在 $y$ 轴上构造点 $K$、$B$,分别记它们的纵坐标为 $k$、$b$,画函数 $y= kx+b$ 的图像.
(2)移动点 $K$,观察函数 $y= kx+b$ 图像发生的变化,你有什么发现?
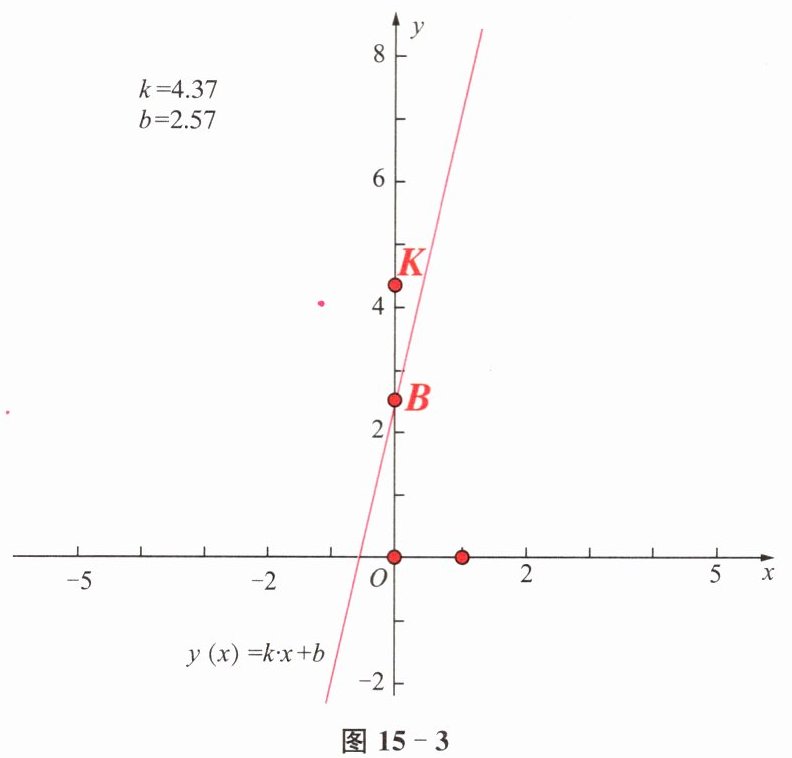
(3)移动点 $B$,观察函数 $y= kx+b$ 图像发生的变化,你有什么发现?
实验指南
本实验是为苏科版《义务教育教科书 数学》八年级上册“6.3 一次函数的图像”而设计的,可以用作教学片断.通过用动态几何软件画一次函数的图像,探索一次函数的图像及其性质.
首先,利用动态几何软件进行静态描点,逐渐增加所绘制的点的个数,观察并猜想一次函数的图像特征.再利用动态几何软件进行动态描点,观察所绘制的点的运动路径,验证一次函数的图像特征.
其次,利用动态几何软件画出一次函数 $y= kx+b$ 的图像并改变 $k$、$b$ 的值,观察相应的一次函数 $y= kx+b$ 图像的变化,得到一次函数 $y= kx+b$ 的图像与 $k$、$b$ 的关系.
(1)填表,并以表中各对 $x$、$y$ 的值为点的坐标,利用动态几何软件建立直角坐标系并构造这些点,如图 15-1.

| $x$ | …$$ | $-3.2$ | $-3$ | $-2.8$ | $-2.6$ | $-2$ | $-0.2$ | $0$ | $0.2$ | $0.4$ | $0.6$ | $0.8$ | $1$ | …$$ |

| $y= 2x+1$ | …$$ | ______ | ______ | ______ | ______ | ______ | ______ | ______ | ______ | ______ | ______ | ______ | ______ | …$$ |
(2)观察这些点,你有什么发现?
(3)再取更多的对应的 $x$、$y$ 值,并在直角坐标系中构造这些点,你有什么发现?
(4)猜想:一次函数 $y= 2x+1$ 的图像是什么图形?
(5)如图 15-2,打开动态几何软件,建立直角坐标系,在 $x$ 轴上构造一个点 $X$,记横坐标为 $x$,绘制动点 $P(x,2x+1)$;移动点 $X$,观察点 $P$ 经过的路径痕迹.你有什么发现?

(6)利用动态几何软件画函数 $y= -x+3$ 的图像.这个图像是什么样的图形?与你的猜想一致吗?
2. 探索一次函数 $y= kx+b$ 图像的性质
(1)打开动态几何软件,建立直角坐标系.如图 15-3,在 $y$ 轴上构造点 $K$、$B$,分别记它们的纵坐标为 $k$、$b$,画函数 $y= kx+b$ 的图像.
(2)移动点 $K$,观察函数 $y= kx+b$ 图像发生的变化,你有什么发现?

(3)移动点 $B$,观察函数 $y= kx+b$ 图像发生的变化,你有什么发现?
实验指南
本实验是为苏科版《义务教育教科书 数学》八年级上册“6.3 一次函数的图像”而设计的,可以用作教学片断.通过用动态几何软件画一次函数的图像,探索一次函数的图像及其性质.
首先,利用动态几何软件进行静态描点,逐渐增加所绘制的点的个数,观察并猜想一次函数的图像特征.再利用动态几何软件进行动态描点,观察所绘制的点的运动路径,验证一次函数的图像特征.
其次,利用动态几何软件画出一次函数 $y= kx+b$ 的图像并改变 $k$、$b$ 的值,观察相应的一次函数 $y= kx+b$ 图像的变化,得到一次函数 $y= kx+b$ 的图像与 $k$、$b$ 的关系.
答案:
【解析】:
本题主要考查一次函数的图像及其性质,通过动态几何软件来直观感受和理解一次函数$y=kx+b$的图像特征以及$k$、$b$对图像的影响。
对于$y = 2x + 1$,
当$x=-3.2$时,$y=2×(-3.2)+1=-6.4 + 1=-5.4$;
当$x = - 3$时,$y=2×(-3)+1=-6 + 1=-5$;
当$x=-2.8$时,$y=2×(-2.8)+1=-5.6 + 1=-4.6$;
当$x=-2.6$时,$y=2×(-2.6)+1=-5.2 + 1=-4.2$;
当$x = - 2$时,$y=2×(-2)+1=-4 + 1=-3$;
当$x=-0.2$时,$y=2×(-0.2)+1=-0.4 + 1=0.6$;
当$x = 0$时,$y=2×0+1=1$;
当$x=0.2$时,$y=2×0.2+1=0.4 + 1=1.4$;
当$x = 0.4$时,$y=2×0.4+1=0.8 + 1=1.8$;
当$x=0.6$时,$y=2×0.6+1=1.2 + 1=2.2$;
当$x = 0.8$时,$y=2×0.8+1=1.6 + 1=2.6$;
当$x = 1$时,$y=2×1+1=3$。
(2)观察这些点,发现这些点似乎在一条直线上。
(3)再取更多的对应的$x$、$y$值,并在直角坐标系中构造这些点,会发现这些点仍然在同一条直线上。
(4)猜想一次函数$y = 2x + 1$的图像是一条直线。
(5)打开动态几何软件,建立直角坐标系,在$x$轴上构造一个点$X$,记横坐标为$x$,绘制动点$P(x,2x + 1)$;移动点$X$,观察点$P$经过的路径痕迹,发现点$P$的路径是一条直线,验证了前面的猜想。
(6)利用动态几何软件画函数$y=-x + 3$的图像,这个图像是一条直线,与前面的猜想一致。
对于探索一次函数$y=kx + b$图像的性质:
(1)打开动态几何软件,建立直角坐标系,在$y$轴上构造点$K$、$B$,分别记它们的纵坐标为$k$、$b$,画函数$y=kx + b$的图像,得到一条直线。
(2)移动点$K$,观察函数$y=kx + b$图像发生的变化,发现$k$的值变化时,直线的斜率发生变化,$k$决定直线的倾斜程度,$k\gt0$时,直线从左到右上升,$k\lt0$时,直线从左到右下降。
(3)移动点$B$,观察函数$y=kx + b$图像发生的变化,发现$b$的值变化时,直线在$y$轴上的截距发生变化,$b$表示直线与$y$轴交点的纵坐标。
【答案】:
(1)$-5.4$;$-5$;$-4.6$;$-4.2$;$-3$;$0.6$;$1$;$1.4$;$1.8$;$2.2$;$2.6$;$3$
(2)这些点似乎在一条直线上。
(3)这些点仍然在同一条直线上。
(4)一次函数$y = 2x + 1$的图像是一条直线。
(5)点$P$的路径是一条直线。
(6)这个图像是一条直线,与猜想一致。
(2)$k$的值变化时,直线的斜率发生变化,$k$决定直线的倾斜程度,$k\gt0$时,直线从左到右上升,$k\lt0$时,直线从左到右下降。
(3)$b$的值变化时,直线在$y$轴上的截距发生变化,$b$表示直线与$y$轴交点的纵坐标。
本题主要考查一次函数的图像及其性质,通过动态几何软件来直观感受和理解一次函数$y=kx+b$的图像特征以及$k$、$b$对图像的影响。
对于$y = 2x + 1$,
当$x=-3.2$时,$y=2×(-3.2)+1=-6.4 + 1=-5.4$;
当$x = - 3$时,$y=2×(-3)+1=-6 + 1=-5$;
当$x=-2.8$时,$y=2×(-2.8)+1=-5.6 + 1=-4.6$;
当$x=-2.6$时,$y=2×(-2.6)+1=-5.2 + 1=-4.2$;
当$x = - 2$时,$y=2×(-2)+1=-4 + 1=-3$;
当$x=-0.2$时,$y=2×(-0.2)+1=-0.4 + 1=0.6$;
当$x = 0$时,$y=2×0+1=1$;
当$x=0.2$时,$y=2×0.2+1=0.4 + 1=1.4$;
当$x = 0.4$时,$y=2×0.4+1=0.8 + 1=1.8$;
当$x=0.6$时,$y=2×0.6+1=1.2 + 1=2.2$;
当$x = 0.8$时,$y=2×0.8+1=1.6 + 1=2.6$;
当$x = 1$时,$y=2×1+1=3$。
(2)观察这些点,发现这些点似乎在一条直线上。
(3)再取更多的对应的$x$、$y$值,并在直角坐标系中构造这些点,会发现这些点仍然在同一条直线上。
(4)猜想一次函数$y = 2x + 1$的图像是一条直线。
(5)打开动态几何软件,建立直角坐标系,在$x$轴上构造一个点$X$,记横坐标为$x$,绘制动点$P(x,2x + 1)$;移动点$X$,观察点$P$经过的路径痕迹,发现点$P$的路径是一条直线,验证了前面的猜想。
(6)利用动态几何软件画函数$y=-x + 3$的图像,这个图像是一条直线,与前面的猜想一致。
对于探索一次函数$y=kx + b$图像的性质:
(1)打开动态几何软件,建立直角坐标系,在$y$轴上构造点$K$、$B$,分别记它们的纵坐标为$k$、$b$,画函数$y=kx + b$的图像,得到一条直线。
(2)移动点$K$,观察函数$y=kx + b$图像发生的变化,发现$k$的值变化时,直线的斜率发生变化,$k$决定直线的倾斜程度,$k\gt0$时,直线从左到右上升,$k\lt0$时,直线从左到右下降。
(3)移动点$B$,观察函数$y=kx + b$图像发生的变化,发现$b$的值变化时,直线在$y$轴上的截距发生变化,$b$表示直线与$y$轴交点的纵坐标。
【答案】:
(1)$-5.4$;$-5$;$-4.6$;$-4.2$;$-3$;$0.6$;$1$;$1.4$;$1.8$;$2.2$;$2.6$;$3$
(2)这些点似乎在一条直线上。
(3)这些点仍然在同一条直线上。
(4)一次函数$y = 2x + 1$的图像是一条直线。
(5)点$P$的路径是一条直线。
(6)这个图像是一条直线,与猜想一致。
(2)$k$的值变化时,直线的斜率发生变化,$k$决定直线的倾斜程度,$k\gt0$时,直线从左到右上升,$k\lt0$时,直线从左到右下降。
(3)$b$的值变化时,直线在$y$轴上的截距发生变化,$b$表示直线与$y$轴交点的纵坐标。
查看更多完整答案,请扫码查看


