1. 探索角平分线的性质
(1)揭下附录1中的三角形纸片,按如图6-1所示的方法折叠.

(2)如图6-2,在△ABC中,BD、PF、PE是1(1)中折叠的折痕.

①∠ABD与∠CBD、PE与PF分别有怎样的数量关系?
②PE与BC、PF与AB分别有怎样的位置关系?
③根据①、②,你有什么发现?
2. 探索角平分线性质的逆定理
(1)揭下附录1中的三角形纸片,按如图6-3所示的方法操作.

(2)如图6-4,在△ABC中,DM、EN分别是2(1)中折叠的折痕,DM与EN的交点为P.
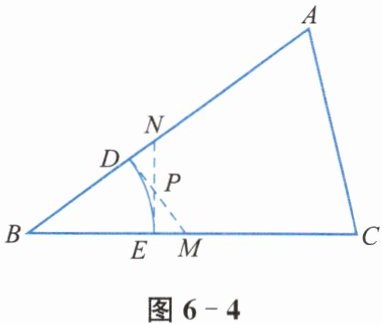
① MD与AB、NE与BC分别有怎样的位置关系?
② PD与PE相等吗?为什么?
③ 折∠ABC的平分线,观察点P是否在这条角平分线上,为什么?
④ 根据①、②、③,你有什么发现?
实验指南
本实验是为苏科版《义务教育教科书 数学》八年级上册“2.4线段、角的轴对称性”而设计的,可以用作教学片段.
首先,通过折纸得到三角形一个角的平分线,并在折痕上任取一点,过该点折这个角两边的垂线,直观感受折痕间的关系,进而探索角平分线的性质定理.
其次,通过折纸找出到角的两边距离相等的点,再折出这个角的平分线,直观判断该点是否在这条角平分线上,并通过说理,探索角平分线性质的逆定理.
名人名言
数学是一种别具匠心的艺术.
——数学家 哈尔莫斯
(1)揭下附录1中的三角形纸片,按如图6-1所示的方法折叠.

(2)如图6-2,在△ABC中,BD、PF、PE是1(1)中折叠的折痕.

①∠ABD与∠CBD、PE与PF分别有怎样的数量关系?
②PE与BC、PF与AB分别有怎样的位置关系?
③根据①、②,你有什么发现?
2. 探索角平分线性质的逆定理
(1)揭下附录1中的三角形纸片,按如图6-3所示的方法操作.

(2)如图6-4,在△ABC中,DM、EN分别是2(1)中折叠的折痕,DM与EN的交点为P.

① MD与AB、NE与BC分别有怎样的位置关系?
② PD与PE相等吗?为什么?
③ 折∠ABC的平分线,观察点P是否在这条角平分线上,为什么?
④ 根据①、②、③,你有什么发现?
实验指南
本实验是为苏科版《义务教育教科书 数学》八年级上册“2.4线段、角的轴对称性”而设计的,可以用作教学片段.
首先,通过折纸得到三角形一个角的平分线,并在折痕上任取一点,过该点折这个角两边的垂线,直观感受折痕间的关系,进而探索角平分线的性质定理.
其次,通过折纸找出到角的两边距离相等的点,再折出这个角的平分线,直观判断该点是否在这条角平分线上,并通过说理,探索角平分线性质的逆定理.
名人名言
数学是一种别具匠心的艺术.
——数学家 哈尔莫斯
答案:
【解析】:1.(2)①由折叠可知$\angle ABD=\angle CBD=\frac{1}{2}\angle ABC$,$PE=PF$。
②$PE\perp BC$,$PF\perp AB$。
③角平分线上的点到角两边的距离相等。
2.(2)①$MD\perp AB$,$NE\perp BC$。
②相等。
理由:连接$BP$,因为$MD\perp AB$,$NE\perp BC$,所以$\angle MDP=\angle EDP = 90^{\circ}$。
由折叠可知$PD=PE$(折叠前后对应线段相等)。
在$Rt\triangle DMP$和$Rt\triangle ENP$中,$\angle MDP=\angle EDP$,$\angle DMP=\angle ENP = 90^{\circ}$,$PD = PE$,根据$AAS$(角角边)可得$Rt\triangle DMP\cong Rt\triangle ENP$,所以$PD=PE$。
③点$P$在$\angle ABC$的平分线上。
理由:因为$MD\perp AB$,$NE\perp BC$,$PD = PE$,根据角平分线性质的逆定理(到角两边距离相等的点在角的平分线上),所以点$P$在$\angle ABC$的平分线上。
④角的内部到角两边距离相等的点在角的平分线上。
【答案】:1.(2)①$\angle ABD=\angle CBD=\frac{1}{2}\angle ABC$,$PE = PF$;②$PE\perp BC$,$PF\perp AB$;③角平分线上的点到角两边的距离相等。
2.(2)①$MD\perp AB$,$NE\perp BC$;②$PD = PE$,理由见解析;③点$P$在$\angle ABC$的平分线上,理由见解析;④角的内部到角两边距离相等的点在角的平分线上。
②$PE\perp BC$,$PF\perp AB$。
③角平分线上的点到角两边的距离相等。
2.(2)①$MD\perp AB$,$NE\perp BC$。
②相等。
理由:连接$BP$,因为$MD\perp AB$,$NE\perp BC$,所以$\angle MDP=\angle EDP = 90^{\circ}$。
由折叠可知$PD=PE$(折叠前后对应线段相等)。
在$Rt\triangle DMP$和$Rt\triangle ENP$中,$\angle MDP=\angle EDP$,$\angle DMP=\angle ENP = 90^{\circ}$,$PD = PE$,根据$AAS$(角角边)可得$Rt\triangle DMP\cong Rt\triangle ENP$,所以$PD=PE$。
③点$P$在$\angle ABC$的平分线上。
理由:因为$MD\perp AB$,$NE\perp BC$,$PD = PE$,根据角平分线性质的逆定理(到角两边距离相等的点在角的平分线上),所以点$P$在$\angle ABC$的平分线上。
④角的内部到角两边距离相等的点在角的平分线上。
【答案】:1.(2)①$\angle ABD=\angle CBD=\frac{1}{2}\angle ABC$,$PE = PF$;②$PE\perp BC$,$PF\perp AB$;③角平分线上的点到角两边的距离相等。
2.(2)①$MD\perp AB$,$NE\perp BC$;②$PD = PE$,理由见解析;③点$P$在$\angle ABC$的平分线上,理由见解析;④角的内部到角两边距离相等的点在角的平分线上。
查看更多完整答案,请扫码查看


