《2024年数学实验手册八年级上册》

1. 观察与验证
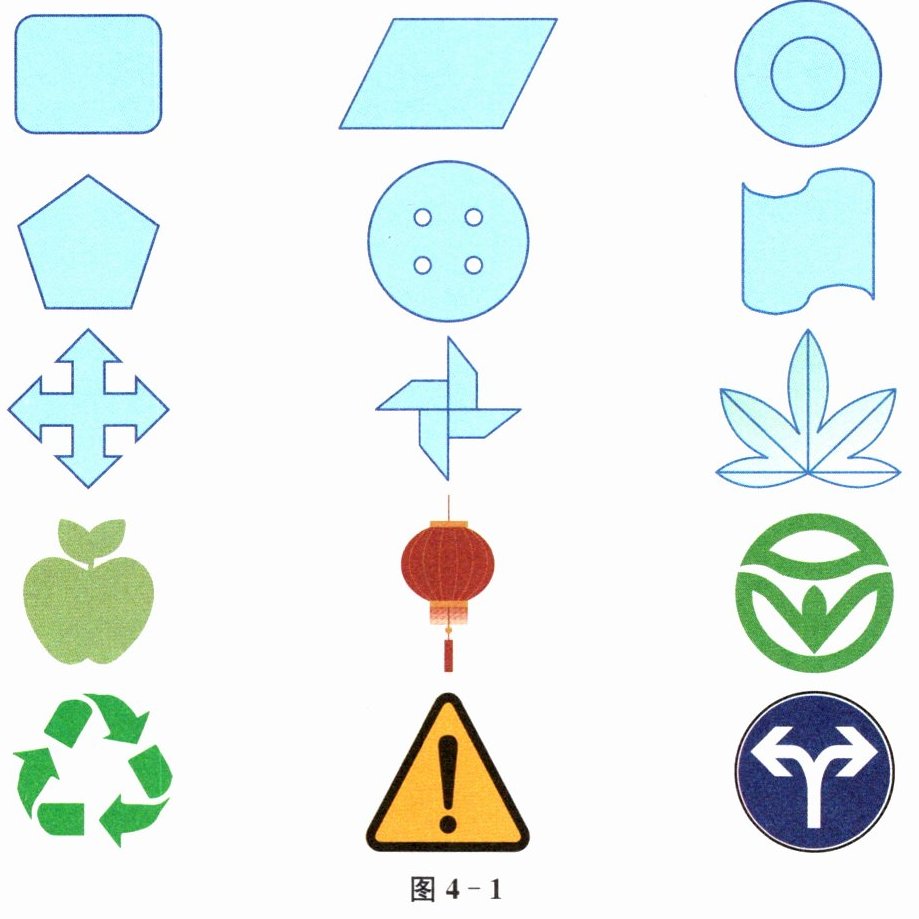
(1)在图4-1中找出轴对称图形(图案).

(2)剪下附录B中相应的透明纸片,通过折叠,验证你的想法.
2. 操作与思考
(1)两人一组,选用两块相同的三角尺摆一摆,使得这两块三角尺关于某条直线对称.
(2)把所摆的图形画在纸上.
(3)通过折叠,验证所摆的两个图形是否成轴对称.
(4)利用两块相同的含有30°角的三角尺,你有多少种摆法,使得同时满足两块三角尺有一边重合、两块三角尺关于重合的边所在直线对称？
＞＞＞ 实验指南
本实验是为苏科版《义务教育教科书 数学》八年级上册“2.1 轴对称与轴对称图形”而设计的,可以用作教学片断.
首先,在“观察与验证”中,经历先观察判断再折纸验证的过程,初步感知折叠与轴对称图形(图案)的联系.
其次,在“操作与思考”中,经历摆一摆、画一画、折一折、想一想等活动,进一步体会折叠与两个图形成轴对称的联系.
＞＞＞ 名人名言
形与数这两者并不是互相割裂的,早在产生数学的萌芽时期,就通过长度、面积与体积的度量而把形与数联系了起来.
——数学家 吴文俊

答案： 1.
(1) 轴对称图形为：正方形、同心圆、正五边形、四孔纽扣、十字箭头、树叶图案、灯笼、绿色圆形图案、蓝色圆形箭头图案。
(2) （通过折叠透明纸片，上述图形沿某条直线折叠后，直线两旁部分能够完全重合，验证正确）。
2.
(1)-
(3) （操作略，所摆图形经折叠验证，沿重合边所在直线折叠后两三角尺完全重合，成轴对称）。
(2) （图形略）。
(4) 3种。