b²(x₁－x₂)2x+a²(y₁－y₂)2y＝0

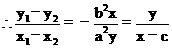
\b²x²+a²y²－b²cx＝0…………(3)

2°当AB垂直于x轴时，点P即为点F，满足方程(3)

故所求点P的轨迹方程为：b²x²+a²y²－b²cx＝0

(2)因为，椭圆　 Q右准线l方程是x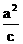＝，原点距l

的距离为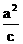，由于c²＝a²－b²，a²＝1+cosq+sinq，b²＝sinq(0<q£)

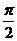则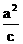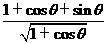＝＝2sin(+)

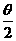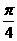当q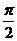＝时，上式达到最大值。此时a²＝2，b²＝1，c＝1，D(2，0)，|DF|＝1

设椭圆Q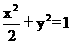：上的点 A(x₁，y₁)、B(x₂，y₂)，三角形ABD的面积

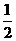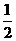S＝|y₁|+|y₂|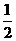＝|y₁－y₂|

设直线m的方程为x＝ky+1，代入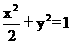中，得(2+k²)y²+2ky－1＝0

由韦达定理得y₁+y₂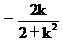＝，y₁y₂＝，

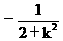4S²＝(y₁－y₂)²＝(y₁+y₂)²－4 y₁y₂＝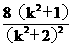

令t＝k²+1³1，得4S²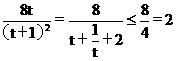＝，当t＝1，k＝0时取等号。

因此，当直线m绕点F转到垂直x轴位置时，三角形ABD的面积最大。

22、(本大题满分14分)

已知数列{a_n}满足：a₁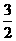＝，且a_n＝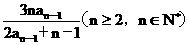

(3)　　　 求数列{a_n}的通项公式；

(4)　　　 证明：对于一切正整数n，不等式a₁·a₂·……a_n<2·n！