5.已知m、n是不重合的直线,α、β是不重合的平面,有下列命题:
①若m α,n∥α,则m∥n;
α,n∥α,则m∥n;
②若m∥α,m∥β,则α∥β;
③若α∩β=n,m∥n,则m∥α且m∥β;
④若m⊥α,m⊥β,则α∥β.
其中真命题的个数是
(A)0 (B)1 (C)2 (D)3
4.已知F1、F2是椭圆的两个焦点,过F1且与椭圆长轴垂直的直线交椭圆于A、B两点,若△ABF2是真正三角形,则这个椭圆的离心率是
(A) (B)
(B)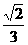 (C)
(C)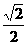 (D)
(D)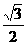
3.命题p:若a、b∈R,则|a|+|b|>1是|a+b|>1的充分而不必要条件;
命题q:函数y=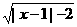 的定义域是(-∞,-1
的定义域是(-∞,-1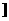 ∪[3,+∞
∪[3,+∞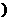 .则
.则
(A)“p或q”为假 (B)“p且q”为真
(C)p真q假 (D)p假q真
(15)(本小题满分14分)
在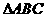 中,
中, ,
, ,
, ,求
,求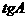 的值和
的值和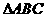 的面积
的面积
(16)(本小题满分14分)
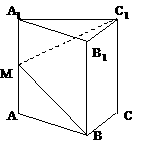
如图,在正三棱柱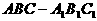 中,AB=2,
中,AB=2, ,由顶点B沿棱柱侧面经过棱
,由顶点B沿棱柱侧面经过棱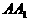 到顶点
到顶点 的最短路线与
的最短路线与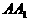 的交点记为M,求:
的交点记为M,求:
(I)三棱柱的侧面展开图的对角线长
(II)该最短路线的长及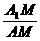 的值
的值
(III)平面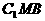 与平面ABC所成二面角(锐角)的大小
与平面ABC所成二面角(锐角)的大小
(17)(本小题满分14分)
如图,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2),A( ),B(
),B( )均在抛物线上。
)均在抛物线上。
(I)写出该抛物线的方程及其准线方程
(II)当PA与PB的斜率存在且倾斜角互补时,求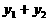 的值及直线AB的斜率
的值及直线AB的斜率

(18)(本小题满分14分)
函数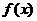 定义在[0,1]上,满足
定义在[0,1]上,满足 且
且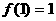 ,在每个区间
,在每个区间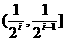 (
(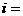 1,2……)上,
1,2……)上, 的图象都是平行于x轴的直线的一部分。
的图象都是平行于x轴的直线的一部分。
(I)求 及
及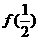 ,
,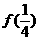 的值,并归纳出
的值,并归纳出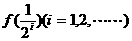 的表达式
的表达式
(II)设直线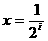 ,
,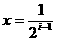 ,x轴及
,x轴及 的图象围成的矩形的面积为
的图象围成的矩形的面积为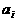 (
(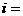 1,2……),求
1,2……),求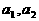 及
及 的值
的值
(19)(本小题满分12分)
某段城铁线路上依次有A、B、C三站,AB=15km,BC=3km,在列车运行时刻表上,规定列车8时整从A站发车,8时07分到达B站并停车1分钟,8时12分到达C站,在实际运行中,假设列车从A站正点发车,在B站停留1分钟,并在行驶时以同一速度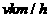 匀速行驶,列车从A站到达某站的时间与时刻表上相应时间之差的绝对值称为列车在该站的运行误差。
匀速行驶,列车从A站到达某站的时间与时刻表上相应时间之差的绝对值称为列车在该站的运行误差。
(I)分别写出列车在B、C两站的运行误差
(II)若要求列车在B,C两站的运行误差之和不超过2分钟,求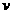 的取值范围
的取值范围
(20)(本小题满分12分)
给定有限个正数满足条件T:每个数都不大于50且总和L=1275。现将这些数按下列要求进行分组,每组数之和不大于150且分组的步骤是:
首先,从这些数中选择这样一些数构成第一组,使得150与这组数之和的差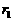 与所有可能的其他选择相比是最小的,
与所有可能的其他选择相比是最小的,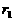 称为第一组余差;
称为第一组余差;
然后,在去掉已选入第一组的数后,对余下的数按第一组的选择方式构成第二组,这时的余差为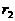 ;如此继续构成第三组(余差为
;如此继续构成第三组(余差为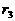 )、第四组(余差为
)、第四组(余差为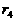 )、……,直至第N组(余差为
)、……,直至第N组(余差为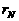 )把这些数全部分完为止。
)把这些数全部分完为止。
(I)判断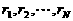 的大小关系,并指出除第N组外的每组至少含有几个数
的大小关系,并指出除第N组外的每组至少含有几个数
(II)当构成第n(n<N)组后,指出余下的每个数与 的大小关系,并证明
的大小关系,并证明
(III)对任何满足条件T的有限个正数,证明:
(9)函数 的最小正周期是______________
的最小正周期是______________
(10)方程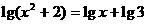 的解是______________
的解是______________
(11)圆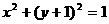 的圆心坐标是______________,如果直线
的圆心坐标是______________,如果直线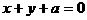 与该圆有公共点,那么实数a的取值范围是______________
与该圆有公共点,那么实数a的取值范围是______________
(12)某地球仪上北纬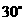 纬线的长度为
纬线的长度为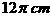 ,该地球仪的半径是__________cm,表面积是______________cm2
,该地球仪的半径是__________cm,表面积是______________cm2
(13)在函数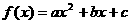 中,若a,b,c成等比数列且
中,若a,b,c成等比数列且 ,则
,则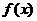 有最______________值(填“大”或“小”),且该值为______________
有最______________值(填“大”或“小”),且该值为______________
(14)定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和。
已知数列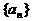 是等和数列,且
是等和数列,且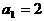 ,公和为5,那么
,公和为5,那么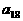 的值为______________,且这个数列的前21项和
的值为______________,且这个数列的前21项和 的值为______________
的值为______________
(1)设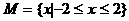 ,
,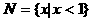 ,则
,则 等于
等于
(A)  (B)
(B)
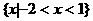
(C) 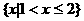 (D)
(D)

(2)满足条件 的复数
的复数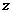 在复平面上对应点的轨迹是
在复平面上对应点的轨迹是
(A) 一条直线 (B) 两条直线 (C) 圆 (D) 椭圆
(3)设m、n是两条不同的直线, 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若 ,
,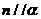 ,则
,则
②若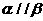 ,
,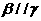 ,
, ,则
,则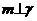
③若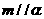 ,
,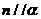 ,则
,则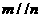
④若 ,
,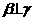 ,则
,则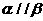
其中正确命题的序号是
(A) ①和② (B) ②和③ (C) ③和④ (D) ①和④
(4)已知a、b、c满足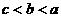 ,且
,且 ,那么下列选项中一定成立的是
,那么下列选项中一定成立的是
(A)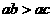 (B)
(B)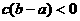 (C)
(C)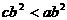 (D)
(D)
(5)从长度分别为1,2,3,4的四条线段中,任取三条的不同取法共有n种,在这些取法中,以取出的三条线段为边可组成的三角形的个数为m,则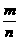 等于
等于
(A) 0 (B)
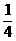 (C)
(C)
 (D)
(D)

(6)如图,在正方体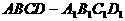 中,P是侧面
中,P是侧面 内一动点,若P到直线BC与直线
内一动点,若P到直线BC与直线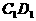 的距离相等,则动点P的轨迹所在的曲线是
的距离相等,则动点P的轨迹所在的曲线是
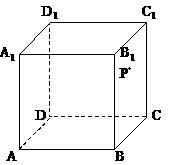
(A) 直线 (B) 圆 (C) 双曲线 (D) 抛物线
(7)函数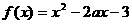 在区间[1,2]上存在反函数的充分必要条件是
在区间[1,2]上存在反函数的充分必要条件是
(A) 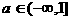 (B)
(B) 
(C) 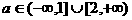 (D)
(D)
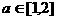
(8)函数 ,其中P、M为实数集R的两个非空子集,又规定
,其中P、M为实数集R的两个非空子集,又规定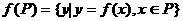 ,
, ,给出下列四个判断:
,给出下列四个判断:
①若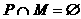 ,则
,则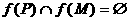
②若 ,则
,则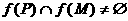
③若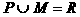 ,则
,则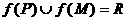
④若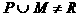 ,则
,则
其中正确判断有
(A) 3个 (B) 2个 (C) 1个 (D) 0个
(17)(本小题满分12分)
已知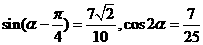 ,求
,求 及
及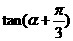 .
.
[思路点拨]本题以三角函数的求值问题考查三角变换能力和运算能力,可从已知角和所求角的内在联系(均含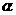 )进行转换得到.
)进行转换得到.
[正确解答]解法一:由题设条件,应用两角差的正弦公式得
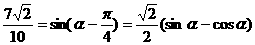 ,即
,即 ①
①
由题设条件,应用二倍角余弦公式得

故 ②
②
由①和②式得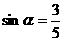 ,
,

因此,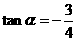 ,由两角和的正切公式
,由两角和的正切公式
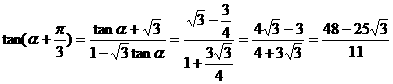
解法二:由题设条件,应用二倍角余弦公式得 ,
,
解得 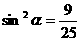 ,即
,即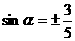

由 可得
可得

由于 ,且
,且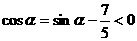 ,故a在第二象限
,故a在第二象限 于是
于是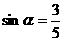 ,
,
从而

以下同解法一
[解后反思]在求三角函数值时,必须对各个公式间的变换应公式的条件要理解和掌握,注意隐含条件的使用,以防出现多解或漏解的情形.
(18)(本小题满分12分)
若公比为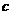 的等比数列
的等比数列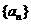 的首项
的首项 且满足
且满足 .
.
(I)求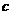 的值;
的值;
(II)求数列 的前
的前 项和
项和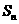 .
.
[思路点拨]本题考查等比数列的通项公式及前n项和的求法.可根据其定义进行求解,要注意①等比数列的公比C是不为零的常数②前n项和的公式是关于n的分段函数,对公比C是否为1加以讨论.
[正确解答](Ⅰ)解:由题设,当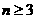 时,
时, ,
,
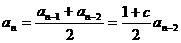 ,
,
由题设条件可得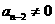 ,因此
,因此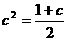 ,即
,即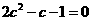

解得c=1或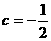

(Ⅱ)解:由(Ⅰ),需要分两种情况讨论,
当c=1时,数列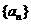 是一个常数列,即
是一个常数列,即 (nÎN*)
(nÎN*)
这时,数列 的前n项和
的前n项和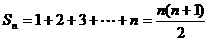

当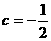 时,数列
时,数列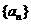 是一个公比为
是一个公比为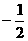 的等比数列,即
的等比数列,即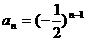 (nÎN*)
(nÎN*)
这时,数列 的前n项和
的前n项和
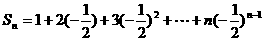 ①
①
① 式两边同乘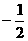 ,得
,得
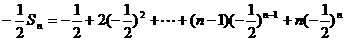 ②
②
①式减去②式,得
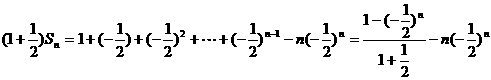
所以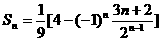 (nÎN*)
(nÎN*)
[解后反思]本题是数列求和及极限的综合题.
(1)完整理解等比数列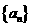 的前n项和公式:
的前n项和公式:
(2)要掌握以下几种情形的极限的求法.①利用 ②利用
②利用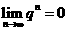 (
( )③要掌握分类讨论的背景转化方法.如
)③要掌握分类讨论的背景转化方法.如 时转化为
时转化为 .
.
(19)(本小题满分12分)
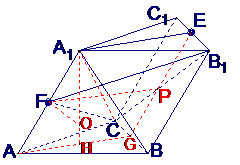 如图,在斜三棱柱
如图,在斜三棱柱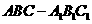 中,
中,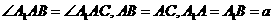 ,
,
侧面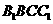 与底面
与底面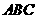 所成的二面角为
所成的二面角为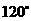 ,
, 分别是棱
分别是棱 的中点
的中点
(I)求 与底面
与底面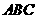 所成的角;
所成的角;
(II)证明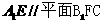 ;
;
(III)求经过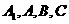 四点的球的体积.
四点的球的体积.
见理第19题
(20)(本小题满分12分)
某人在山坡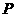 点处观看对面山顶上的一座铁塔,如图所示,塔高
点处观看对面山顶上的一座铁塔,如图所示,塔高 米,塔所在的山高
米,塔所在的山高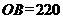 米,
米,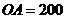 米,图中所示的山坡可视为直线
米,图中所示的山坡可视为直线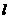 且点
且点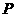 在直线
在直线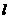 上,
上,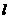 与水平面的夹角为
与水平面的夹角为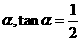 .试问,此人距水平地面多高时,观看塔的视角
.试问,此人距水平地面多高时,观看塔的视角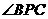 最大(不计此人身高)?
最大(不计此人身高)?
见理第20题
(21)(本小题满分14分)
已知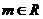 ,设
,设
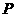 :
: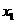 和
和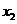 是方程
是方程 的两个实根,不等式
的两个实根,不等式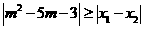 对任意实数
对任意实数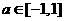 恒成立;
恒成立;
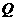 :函数
:函数 在
在 上有极值.
上有极值.
求使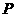 正确且
正确且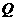 正确的
正确的 的取值范围.
的取值范围.
[思路点拨]本题是组合题,考查一元二次方程的根的概念和导数的应用.
[正确解答] (Ⅰ)由题设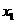 和
和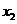 是方程
是方程 的两个实根,得
的两个实根,得
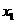 +
+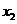 =
=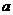 且
且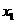
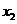 =-2,
=-2,
所以,
当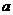 Î[-1,1]时,
Î[-1,1]时,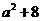 的最大值为9,即
的最大值为9,即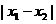 £3
£3
由题意,不等式 对任意实数
对任意实数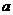 Î[1,1]恒成立的m的解集等于不等式
Î[1,1]恒成立的m的解集等于不等式 的解集
的解集 由此不等式得
由此不等式得
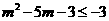 ①
①
或 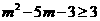 ②
②
不等式①的解为

不等式②的解为 或
或

因为,对 或
或 或
或 时,P是正确的
时,P是正确的
(Ⅱ)对函数 求导
求导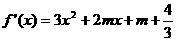
令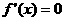 ,即
,即
 此一元二次不等式的判别式
此一元二次不等式的判别式


若D=0,则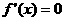 有两个相等的实根
有两个相等的实根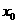 ,且
,且 的符号如下:
的符号如下:
|
|
(-¥,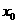 ) ) |
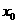 |
(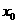 ,+¥) ,+¥) |
|
|
+ |
0 |
+ |
因为, 不是函数
不是函数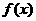 的极值
的极值
若D>0,则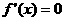 有两个不相等的实根
有两个不相等的实根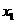 和
和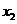 (
(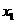 <
<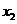 ),且
),且 的符号如下:
的符号如下:
|
x |
(-¥,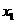 ) ) |
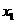 |
(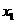 , ,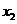 ) ) |
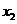 |
(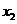 ,+¥) ,+¥) |
 |
+ |
0 |
- |
0 |
+ |
因此,函数f(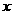 )在
)在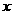 =
=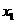 处取得极大值,在
处取得极大值,在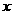 =
=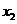 处取得极小值
处取得极小值
综上所述,当且仅当D>0时,函数f(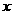 )在(-¥,+¥)上有极值
)在(-¥,+¥)上有极值
由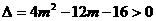 得
得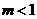 或
或 ,
,
因为,当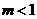 或
或 时,Q是正确得
时,Q是正确得
综上,使P正确且Q正确时,实数m的取值范围为(-¥,1)È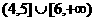

[解后反思]对恒成立问题的等价转换,相应知识的完整理解是关键.对P来说,转化为求使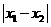 的最大值时的范围,而要注意一次二次方程根存在的充要条件.对Q来说,
的最大值时的范围,而要注意一次二次方程根存在的充要条件.对Q来说,
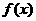 的导函数存在的充要条件的理解是一难点,也是易错点.
的导函数存在的充要条件的理解是一难点,也是易错点.
(22)(本小题满分14分)
抛物线 的方程为
的方程为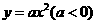 ,过抛物线
,过抛物线 上的一点
上的一点 作斜率为
作斜率为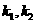 的两条直线分别交抛物线
的两条直线分别交抛物线 于
于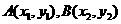 两点(
两点(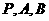 三点互不相同),且满足
三点互不相同),且满足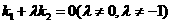 .
.
(I)求抛物线 的焦点坐标和准线方程;
的焦点坐标和准线方程;
(II)设直线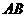 上一点
上一点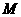 ,满足
,满足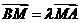 ,证明线段
,证明线段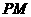 的中点在
的中点在 轴上;
轴上;
(III)当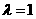 时,若点
时,若点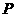 的坐标为(1,-1),求
的坐标为(1,-1),求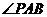 为钝角时点
为钝角时点 的纵坐标
的纵坐标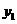 的取值范围.
的取值范围.
见理第22题.

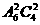 (B)
(B) (C)
(C) (D)
(D)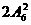
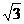 (C)4 (D)
(C)4 (D)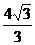
 的值是
的值是 