(11)二项式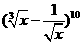 的展开式中常数项为
.
的展开式中常数项为
.
[思路点拨]本题考查二项式定理的通项公式,只要概念清楚和运算无误即可.
[正确解答]展开式的一般项为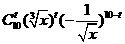 ,令
,令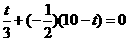 ,
,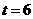 ,因此常数项为
,因此常数项为 .
.
[解后反思]要注意符号因子不能丢.
(12)已知 ,
,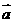 和
和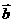 的夹角为
的夹角为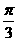 ,以
,以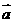 ,
,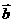 为邻边作平行四边形,则此平行四边形的两条对角线中较短的一条的长度为
.
为邻边作平行四边形,则此平行四边形的两条对角线中较短的一条的长度为
.
[思路点拨]本题以向量为背景,考查余弦定理,要判断较短的一条应是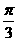 所对的对角线.
所对的对角线.
[正确解答]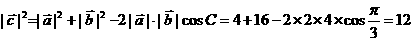
[解后反思]要正确向量的加减法则的几何意义,对向量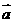 =(x,y)的模有几种方法.①
=(x,y)的模有几种方法.①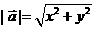 ②
② .
.
 (13)如图,
(13)如图,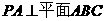 ,
,
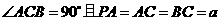 ,
,
则异面直线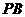 与
与 所成的角的正切值等于
.
所成的角的正切值等于
.
见理第12题
(14)在数列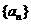 中,
中, ,且
,且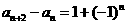
 ,则
,则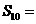 .
.
见理第13题
(15)设函数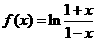 ,则函数
,则函数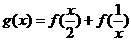 的定义域为
.
的定义域为
.
[思路点拨]本题考查复合函数定义域的求法,必须使常见各类函数都有意义,构成不等式组来解.
[正确解答]由题意得
 则所求定义域为
则所求定义域为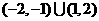 .
.
 [解后反思]正确地解不等式组,将繁分式化简是一关键.
[解后反思]正确地解不等式组,将繁分式化简是一关键.
(16)在三角形的每条边上各取三个分点(如图).以
这9个分点为顶点可画出若干个三角形,若从中
任意抽取一个三角形,则其三个顶点分别落在原
三角形的三个不同边上的概率为 .
[思路点拨]本题考查等可能事件的概率,关键是要确定基本事件.
[正确解答]可画出的三角形个数为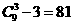 ,三个顶点分别落在不同边上的个数为
,三个顶点分别落在不同边上的个数为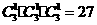 ,所求概率为
,所求概率为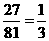 .
.
[解后反思]理解和掌握等可能事件的概率的计算公式P(A)= ,本题中构成三角形的个数是一难点.
,本题中构成三角形的个数是一难点.
22、(本小题满分14分)
设函数
(Ⅰ)证明 其中为k为整数
其中为k为整数
(Ⅱ)设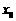 为
为 的一个极值点,证明
的一个极值点,证明
(Ⅲ)设 在(0,+∞)内的全部极值点按从小到大的顺序排列为
在(0,+∞)内的全部极值点按从小到大的顺序排列为 ,证明:
,证明: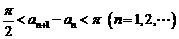
2005年普通高等学校招生全国统一考试(天津卷)
21、(本题14分)
抛物线C的方程为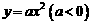 ,过抛物线C上一点
,过抛物线C上一点 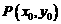 (
( )作斜率为
)作斜率为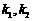 的两条直线分别交抛物线C于
的两条直线分别交抛物线C于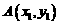 ,
,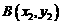 两点(P、A、B三点互不相同),且满足
两点(P、A、B三点互不相同),且满足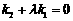 (
(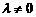 ≠0且
≠0且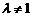 )。
)。
(Ⅰ)求抛物线C的焦点坐标和准线方程
(Ⅱ)设直线AB上一点M,满足 ,证明线段PM的中点在y轴上
,证明线段PM的中点在y轴上
(Ⅲ)当 时,若点P的坐标为(1,
时,若点P的坐标为(1,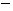 1),求∠PAB为钝角时点A的纵坐标
1),求∠PAB为钝角时点A的纵坐标 的取值范围。
的取值范围。
20、(本小题满分12)
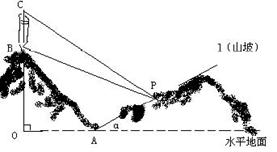
某人在一山坡P处观看对面山项上的一座铁塔,如图所示,塔高BC = 80(米),塔所在的山高OB = 220(米),OA = 200(米),图中所示的山坡可视为直线l且点P在直线l上,l与水平地面的夹角为a,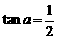 。试问此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)。
。试问此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)。
19、(本小题满分12分)
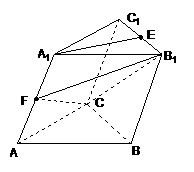
如图,在斜三棱柱 中,
中, ,
,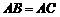 ,侧面
,侧面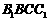 与底面ABC所成的二面角为120
与底面ABC所成的二面角为120 ,E、F分别是棱
,E、F分别是棱 、
、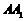 的中点。
的中点。
(Ⅰ)求 与底面ABC所成的角;
与底面ABC所成的角;
(Ⅱ)证明EA∥平面 ;
;
 (Ⅲ)求经过
(Ⅲ)求经过 、A、B、C四点的球的体积。
、A、B、C四点的球的体积。
15、某公司有5万元资金用于投资开发项目,如果成功,一年后可获利12%,一旦失败,一年后将丧失全部资金的50%,下表是过去200例类似项目开发的实施结果:
|
投资成功 |
投资失败 |
|
192次 |
8次 |
则该公司一年后估计可获收益的期望是__________(元)。
14、在直角坐标系xOy中,已知点A (0,1)和点B (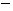 3,4),若点C在∠AOB的平分线上且| OC | = 2,则OC = __________。
3,4),若点C在∠AOB的平分线上且| OC | = 2,则OC = __________。

 。
。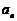 }的前n项和
}的前n项和 ;
; 。
。
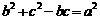 和
和 。求∠A和
。求∠A和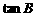 的值。
的值。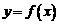 的图象关于直线
的图象关于直线 对称,则
对称,则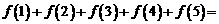 __________。
__________。