4.已知点P(x,y)在不等式组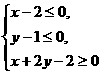 表示的平面区域上运动,则z=x-y的取值
表示的平面区域上运动,则z=x-y的取值
范围是 ( )
A.[-2,-1] B.[-2,1] C.[-1,2] D.[1,2]
 5.如图,正方体ABCD-A1B1C1D1的棱长为1,O是底面
5.如图,正方体ABCD-A1B1C1D1的棱长为1,O是底面
A1B1C1D1的中心,则O到平面AB C1D1的距离为 ( )
A. B.
B.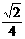
C.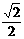 D.
D.
(17)本小题主要考查复数模、辐角和等比中项的概念,考查运算能力,满分12分。
解:设 ,则复数z的实部为
,则复数z的实部为 .
.
∴ 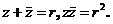
由题设
即 
∴ 
整理得 r2+2r-1=0.
解得 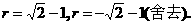
即 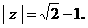
(18)本小题主要考查线面关系和直棱柱等基础知识,同时考查空间想像能力和推理运算能力,满分12分.
(Ⅰ)解:连结BG,则BG是BE在面ABD的射影,即∠EBG是A1B与平面ABD所成的角.
设F为AB中点,连结EF、FC,
∵ D、E分别是CC1、A1B的中点,又DC⊥平面ABC,
 ∴ CDEF为矩形.
∴ CDEF为矩形.
连结DF,G是△ADB的重心,∴G∈DF.在直角三角形EFD中, ,
,
∵EF=1,∴
于是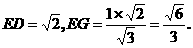
∵ 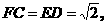
∴ 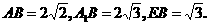
∴ 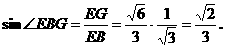
∴ A1B与平面ABD所成的角是
(Ⅱ)解法一:∵ ED⊥AB,ED⊥EF,又EF∩AB=F.
∴ ED⊥面A1AB,
又ED∈面AED,
∴ 平面AED⊥平面A1AB,且面AED∩平面A1AB=AE.
作A1k⊥AE,垂足为k,
∴ A1k⊥平面AED.即A1k是A1到平面AED的距离.
在△A1AB1中,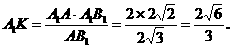
∴ A1到平面AED的距离为
解法二:连结A1D,有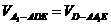
∵ ED⊥AB,ED⊥EF,又EF∩AB=F,
∴ ED⊥平面A1AB.
设A1到平面AED的距离为h.
则 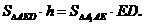
又 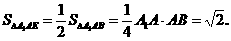
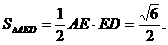
∴ 
即A1到平面AED的距离为
(19)本小题主要考查集合、函数、不等式、绝对值等基础知识,考查分析和判断能力,满分12分.
解:函数y=cx在R上单调递减
不等式x+| x-2c | >1的解集为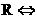 函数y=x+| x-2c | 在R上恒大于1,
函数y=x+| x-2c | 在R上恒大于1,
∵ 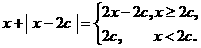
∴ 函数y=x+| x-2c | 在R上的最小值为2c.
∴ 不等式x+| x-2c | >1的解集为
如果P正确,且Q不正确,则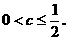
如果P不正确,且Q正确,则c≥1.
所以c的取值范围为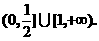
(20)本小题主要考查利用余弦定理解斜三角形的方法,根据所给条件选择适当坐标系和圆的方程等基础知识,考查运用所学知识解决实际问题能力,满分12分.
 解法一:设在时刻t(h)台风中心为Q,此时台风侵袭的圆形区域半径为10t+60 (km).
解法一:设在时刻t(h)台风中心为Q,此时台风侵袭的圆形区域半径为10t+60 (km).
若在时刻t城市O受到台风的侵袭,则OQ≤10t+60.
由余弦定理知

由于 PO=300,PQ=20t,
cos∠OPQ=cos(θ-45°)
=cosθcos45°+sinθsin45°
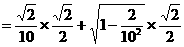
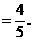
 故
故 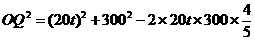

因此 202t2-9600t+3002≤(10t+60)2,
即 t2-36t+288≤0,
解得 12≤t≤24.
答:12小时后该城市开始受到台风的侵袭.
解法二:如图建立坐标系:以O为原点,正东方向为x轴正向,
在时刻t(h)台风中心 的坐标为
的坐标为
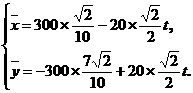
此时台风侵袭的区城是
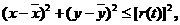
其中r(t)=10t+60.
若在t时刻城市O受到台风的侵袭,则有
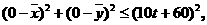
即 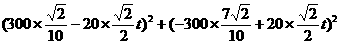
≤(10t+60)2,
即 r2-36t+288≤0,
解得 12≤t≤24.
答:12小时后该城市开始受到台风的侵袭.
(21)本小题主要考查根据已知条件求轨迹的方法,椭圆的方程和性质,利用方程判定曲线的性质,曲线与方程的关系等解析几何的基本思想和综合解题能力,满分14分.
解:根据题设条件,首先求出点P坐标满足的方程,据此再判断是否存在两定点,使得点P到两定点距离的和为定值.
按题意有A(-2,0),B(2,0),C(2,4a),D(-2,4a).
设
由此有E(2,4ak),F(2-4k,4a),G(-2, 4a-4ak).
直线OF的方程为:2ax+(2k-1)y=0, ①
直线GE的方程为:-a (2k-1) x+y-2a=0. ②
从①、②消去参数k,得点P(x,y)坐标满足方程2a2x2+y2-2ay=0.
整理得

当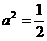 时,点P的轨迹为圆弧,所以不存在符合题意的两点.
时,点P的轨迹为圆弧,所以不存在符合题意的两点.
当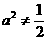 时,点P的轨迹为椭圆的一部分,点P到该椭圆焦点的距离的和为定长.
时,点P的轨迹为椭圆的一部分,点P到该椭圆焦点的距离的和为定长.
当 时,点P的椭圆两个焦点
时,点P的椭圆两个焦点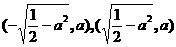 的距离之和为定值
的距离之和为定值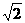
当 时,点P的椭圆两个焦点
时,点P的椭圆两个焦点 的距离之和为定值2a.
的距离之和为定值2a.
(22)本小题主要考查数列,排列组合概念等知识,考查分析问题和解决问题的能力,满分12分.
(Ⅰ)解:(i)第四行 17 18 20 24
第五行 33 34 36 40 48
(ii)解法一:设 ,只须确定正整数t0,s0
,只须确定正整数t0,s0
数列{an}中小于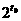 的项构成的子集为
的项构成的子集为
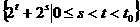 ,
,
其元素个数为 
依题意 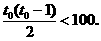
满足上式的最大整数t0为14,所以取t0=14.
因为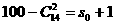 ,由此解得s0=8.
,由此解得s0=8.
∴ a 100=214+28=16640.
解法二:n为an的下标.
三角形数表第一行第一个元下标为1.
第二行第一个元下标为
……
第t行第一个元下标为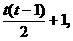 第t行第s个元下标为
第t行第s个元下标为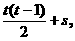 该元等于2t+2t-1.
该元等于2t+2t-1.
据此判断a100所在的行.
因为 ,所以a100是三角形表第14行的第9个元
,所以a100是三角形表第14行的第9个元
a100=214+29-1=16640.
(Ⅱ)(本小题为附加题,如果解答正确,加4分,但全卷总分不超过150分)
解:bk=1160=210+27+23.
令 M={c∈B | c
<1160} (其中,B= ).
).
因M={c∈B | c <210}∪{c∈B | 210 < c<210+27}
∪{c∈B | 210+27< c<210+27+23}.
现在求M的元素个数:
{c∈B | c
<210}= ,
,
其元素个数为 ;
;
{c∈B | 210 < c <210+27}={210+2s+2r | 0≤r<s<7}
其元素个数为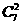 ;
;
{c∈B | 210+27 < c <210+27+23 }={210+27+2r | 0≤r<3},
其元素个数为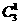 .
.

(17)(本小题满分12分)
已知复数z的辐角为60°,且| z-1 |是| z |和| z-2 |的等比中项,求| z |.
(18)(本小题满分12分)
如图,在直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90°.侧棱AA1=2,D、E分别CC1与A1B的中点,点E在平面ABD上的射影是△ABD的重心G.
 (Ⅰ)求A1B与平面ABD所成角的大小(结果用反三角函数值表示);
(Ⅰ)求A1B与平面ABD所成角的大小(结果用反三角函数值表示);
(Ⅱ)求点A1到平面AED的距离.
(19)(本小题满分12分)
已知c>0,设
P:函数y=cx在R上单调递减.
Q:不等式x+| x-2c | > 1 的解集为R.
如果P和Q有且仅有一个正确,求c的取值范围.
 (20)(本小题满分12分)
(20)(本小题满分12分)
在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南 方向300 km的海面P处,并以20 km/h的速度向西偏北45°方向移动.台风侵袭的范围为圆形区域,当前半径为60 km,并以10 km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?
方向300 km的海面P处,并以20 km/h的速度向西偏北45°方向移动.台风侵袭的范围为圆形区域,当前半径为60 km,并以10 km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?
 (21)(本小题满分14分)
(21)(本小题满分14分)
已知常数a > 0,在矩形ABCD中,AB=4,BC=4a,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且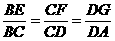 ,P为GE与OF的交点(如图).问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由.
,P为GE与OF的交点(如图).问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由.
(22)(本小题满分12分,附加题4分)
(Ⅰ)设{an}是集合 中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,……
中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,……
将数列{an}各项按照上小下大,左小右大的原则写成如下的三角形数表:

(i)写出这个三角形数表的第四行、第五行各数;
(ii)求a100.
(Ⅱ)(本小题为附加题,如果解答正确,加4分,但全卷总分不超过150分)
设{bn}是集合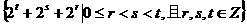 中所有的数从小到大排列成的数列,已知bk
=1160,求k.
中所有的数从小到大排列成的数列,已知bk
=1160,求k.
普通高等学校招生全国统一考试
数学试题(理工农医类)参考解答及评分标准
(13)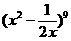 展开式中x9的系数是
.
展开式中x9的系数是
.
(14)使log2(-x)<x+1成立的x的取值范围是 .
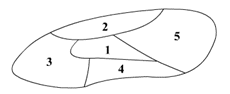 (15)如图,一个地区分为5个行政区域,现给地
图着色,要求相邻区域不得使用同一颜色,现有4种颜色可供选择,则不同的着色方法共有
种.(以数字作答)
(15)如图,一个地区分为5个行政区域,现给地
图着色,要求相邻区域不得使用同一颜色,现有4种颜色可供选择,则不同的着色方法共有
种.(以数字作答)
 (16)下列五个正方体图形中,l是正方体的一条对角线,点M、N、P分别为其所在棱的中点,能得出l⊥面MNP的图形的序号是
.(写出所有符合要求的图形序号)
(16)下列五个正方体图形中,l是正方体的一条对角线,点M、N、P分别为其所在棱的中点,能得出l⊥面MNP的图形的序号是
.(写出所有符合要求的图形序号)
(1)已知 ,则tg 2x=
,则tg 2x=
(A) (B)
(B)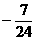 (C)
(C)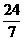 (D)
(D)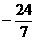
(2)圆锥曲线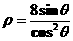 的准线方程是
的准线方程是
(A) (B)
(B)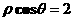 (C)
(C) (D)
(D)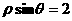
(3)设函数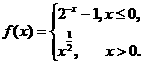 若f(x0)>1,则x0的取值范围是
若f(x0)>1,则x0的取值范围是
(A)(-1,1) (B)(-1,+∞)
(C)(-∞,-2)∪(0,+∞) (D)(-∞,-1)∪(1,+∞)
(4)函数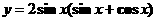 的最大值为
的最大值为
(A) (B)
(B) (C)
(C)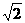 (D)2
(D)2
(5)已知圆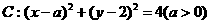 及直线
及直线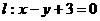 .当直线l被C截得的弦长为
.当直线l被C截得的弦长为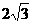 时,则a=
时,则a=
(A)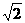 (B)
(B)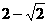 (C)
(C) (D)
(D)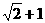
(6)已知圆锥的底面半径为R,高为3R,在它的所有内接圆柱中,全面积的最大值是
(A) (B)
(B) (C)
(C)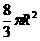 (D)
(D)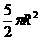
(7)已知方程 的四个根组成一个首项为
的四个根组成一个首项为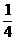 的等差数列,则
的等差数列,则
(A)1
(B)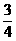 (C)
(C) (D)
(D)
(8)已知双曲线中心在原点且一个焦点为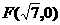 ,直线
,直线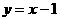 与其相交于M、N两点,MN中点的横坐标为
与其相交于M、N两点,MN中点的横坐标为 ,则此双曲线的方程是
,则此双曲线的方程是
(A) (B)
(B)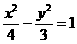 (C)
(C) (D)
(D)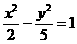
(9)函数f (x)=sinx,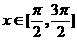 的反函数f-1(x)=
的反函数f-1(x)=
(A)-arcsinx,x∈[-1,1] (B)―π―arcsinx,x∈[-1,1]
(C)π+arcsinx,x∈[-1,1] (D)π-arcsinx,x∈[-1,1]
(10)已知长方形的四个顶点A(0,0),B(2,0),C(2,1)和D(0,1),一质点从AB的中点P0沿与AB夹角为θ的方向射到BC上的点P1后,依次反射到CD、DA和AB上的点P2、P3和P4(入射角等于反射角).设P4的坐标为(x4,0).若1< x4<2,则tgθ的取值范围是
(A)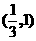 (B)
(B)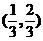 (C)
(C)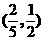 (D)
(D)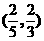
(11)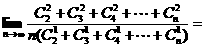
(A)3 (B) (C)
(C)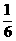 (D)6
(D)6
(12)一个四面体的所有棱长都为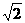 ,四个顶点在同一球面上,则此球的表面积为
,四个顶点在同一球面上,则此球的表面积为
(A)3π (B)4π
(C)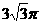 (D)6π
(D)6π
第Ⅱ卷(非选择题 共90分)

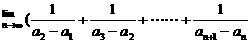 = ( )
= ( ) C.1 D.
C.1 D. 的定义域是 ( )
的定义域是 ( )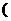 -∞,0] B.[0,+∞
-∞,0] B.[0,+∞ C.(-∞,0) D.(-∞,+∞)
C.(-∞,0) D.(-∞,+∞) (14)(-1,0) (15)72
(16)①④⑤
(14)(-1,0) (15)72
(16)①④⑤