科目:,来源:,题型:
22、已知函数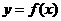 的定义域为
的定义域为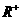 ,对任意
,对任意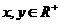 ,有恒等式
,有恒等式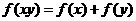 ;且当
;且当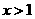 时,
时,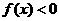 .
.
(1)求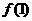 的值;
的值;
(2)求证:当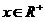 时,恒有
时,恒有 ;
;
(3)求证: 上为减函数;
上为减函数;
[以下(4)小题选理科的学生做;选文科的学生不做]
(4)由上一小题知: 上的减函数,因而
上的减函数,因而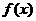 的反函数
的反函数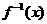 存在,试根据已知恒等式猜想
存在,试根据已知恒等式猜想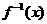 具有的性质,并给出证明.
具有的性质,并给出证明.
高考模拟考
数 学 试 卷
(完卷时间:120分钟 满分:150分) 2006.4.20上午
点击展开完整题目
试题详情
科目:,来源:,题型:
21、已知抛物线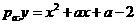 (
(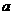 为实常数).
为实常数).
(1)求所有抛物线 的公共点坐标;
的公共点坐标;
(2)当实数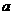 取遍一切实数时,求抛物线
取遍一切实数时,求抛物线 的焦点方程.
的焦点方程.
[理](3)是否存在一条以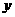 轴为对称轴,且过点
轴为对称轴,且过点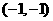 的开口向下的抛物线,使它与某个
的开口向下的抛物线,使它与某个 只有一个公共点?若存在,求出所有这样的
只有一个公共点?若存在,求出所有这样的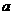 ;若不存在,说明理由.
;若不存在,说明理由.
[文](3)是否存在直线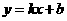 (
(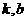 为实常数),使它与所有的抛物线
为实常数),使它与所有的抛物线 都有公共点?若存在,求出所有这样的直线;若不存在,说明理由.
都有公共点?若存在,求出所有这样的直线;若不存在,说明理由.
点击展开完整题目
试题详情
科目:,来源:,题型:
20、某厂2006年拟举行促销活动,经调查测算,该厂产品的年销售量(即该厂的年产量) 万件与去年促销费
万件与去年促销费 (万元)(
(万元)( )满足
)满足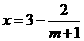 .已知2006年生产的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
.已知2006年生产的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将2006年该产品的利润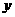 万元表示为年促销费
万元表示为年促销费 (万元)的函数;
(万元)的函数;
(2)求2006年该产品利润的最大值,此时促销费为多少万元?
点击展开完整题目
试题详情
科目:,来源:,题型:
19、 [理]在直棱柱
[理]在直棱柱 中,已知
中,已知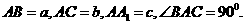
(1)求使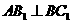 的充要条件(用
的充要条件(用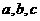 表示);
表示);
(2)求证 为锐角;
为锐角;
(3)若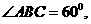 则
则 是否可能为
是否可能为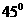 ?证明你的结论.
?证明你的结论.
[文]设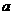 为正数,直角坐标平面内的点集
为正数,直角坐标平面内的点集
(1)画出A所表示的平面区域;
(2)在平面直角坐标系中,规定 时,
时,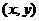 称为格点,当
称为格点,当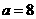 时,A内有几个格点(本小题只要直接写出结果即可);
时,A内有几个格点(本小题只要直接写出结果即可);
(3)点集A连同它的边界构成的区域记为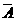 ,若圆
,若圆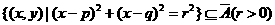 ,求
,求 的最大值.
的最大值.
点击展开完整题目
试题详情

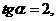 则
则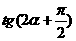 的值是
的值是 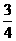 .
.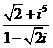 =
= 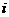 .
.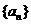 的通项公式为
的通项公式为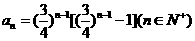 .求
.求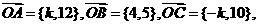 且A、B、C三点共线,求
且A、B、C三点共线,求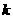 的值.
的值.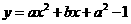 的图像为下列之一,
的图像为下列之一,
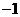 C.
C.
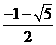 D.
D.
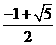
 ,b=
,b= ,若以a,b为边作三角形,则a边所对的角A的取值范围为( )
,若以a,b为边作三角形,则a边所对的角A的取值范围为( ) B .
B . C.
C. 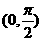 D.
D.