4．[答案]：C

　　　　　 [评述]：本题考查了性规划中最优解问题，“由角点法”可求得目标函数的取值范

　 　　　　　　　　　 围。

[解析]：由线性约束条件画出可行域，救出三个角点分别为(0，1)，(2，1)(2，0)

代入目标函数救出z=x-y的取值范围为[-1，2]

3．[答案]：C

　　　　 [评析]：本题考查了等差数列，等比数列的通项公式和求和公式及数列极限相关交汇知识。

　　　　　　 [解析]：由题意得：,求得d=1,

　　　 　　　　则

　　　　　　　　　　　 又由

　　　　　　　　　　　 所以

　　　　　　　　　　　　　　　　 =

　　　　　　　 所以 故选C。

2．答案：A

　 [评述]：本题考查函数的定义域，指数函数的性质等到知识点。

　 　[解析]:　 由题意得：,故选A.

1.[答案]：B

　　　 [评述[：本题考查复数，复数的意义及其运算。

　　　 [解析]：。故选B。

21．(本小题满分14分)

　　 已知函数f(x)＝lnx，g(x)＝ax²+bx，a≠0.

　 (Ⅰ)若b＝2，且h(x)＝f(x)－g(x)存在单调递减区间，求a的取值范围；

　 (Ⅱ)设函数f(x)的图象C₁与函数g(x)图象C₂交于点P、Q，过线段PQ的中点作x轴的垂线分别交C₁，C₂于点M、N，证明C₁在点M处的切线与C₂在点N处的切线不平行.

普通高等学校招生统一考试

　　　　　 第Ⅰ卷

20．(本小题满分14分)

　　　 自然状态下的鱼类是一种可再生资源，为持续利用这一资源，需从宏观上考察其再生能力及捕捞强度对鱼群总量的影响. 用x_n表示某鱼群在第n年年初的总量，n∈N^*，且x₁＞0.不考虑其它因素，设在第n年内鱼群的繁殖量及捕捞量都与x_n成正比，死亡量与x_n²成正比，这些比例系数依次为正常数a，b，c.

　 (Ⅰ)求x_n+1与x_n的关系式；

　 (Ⅱ)猜测：当且仅当x₁，a，b，c满足什么条件时，每年年初鱼群的总量保持不变？(不

要求证明)

　 (Ⅱ)设a＝2，b＝1，为保证对任意x₁∈(0,2)，都有x_n＞0，n∈N^*，则捕捞强度b的

　　　　 最大允许值是多少？证明你的结论.

19．(本小题满分14分)

　　 已知椭圆C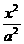：+＝1(a＞b＞0)的左．右焦点为F₁、F₂，离心率为e. 直线

l：y＝ex+a与x轴．y轴分别交于点A、B，M是直线l与椭圆C的一个公共点，P是点F₁关于直线l的对称点，设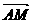＝λ.

　 (Ⅰ)证明：λ＝1－e²；

　 (Ⅱ)确定λ的值，使得△PF₁F₂是等腰三角形.

18．(本小题满分14分)

　　　 某城市有甲、乙、丙3个旅游景点，一位客人游览这三个景点的概率分别是0.4，0.5，0.6，且客人是否游览哪个景点互不影响，设ξ表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值.

(Ⅰ)求ξ的分布及数学期望；

(Ⅱ)记“函数f(x)＝x²－3ξx+1在区间[2，+∞上单调递增”为事件A，求事件A的概率.

17．(本题满分12分)

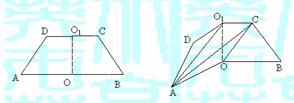　 　　 如图1，已知ABCD是上．下底边长分别为2和6，高为的等腰梯形，将它沿对称轴OO₁折成直二面角，如图2.

　(Ⅰ)证明：AC⊥BO₁；

(Ⅱ)求二面角O－AC－O₁的大小.

16．(本小题满分12分)

　　　 已知在△ABC中，sinA(sinB+cosB)－sinC＝0，sinB+cos2C＝0，求角A、B、C的大小.