(17) (本小题满分12分)
已知函数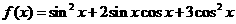 ,
,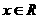 .求:
.求:
(I) 函数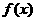 的最大值及取得最大值的自变量
的最大值及取得最大值的自变量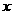 的集合;
的集合;
(II) 函数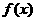 的单调增区间.
的单调增区间.
[解析](I) 解法一:
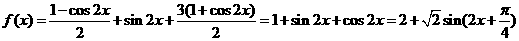
 当
当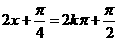 ,即
,即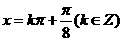 时,
时, 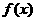 取得最大值
取得最大值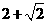 .
.
函数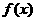 的取得最大值的自变量
的取得最大值的自变量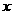 的集合为
的集合为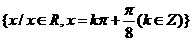 .
.
解法二:
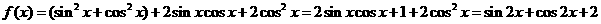
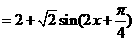
 当
当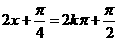 ,即
,即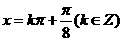 时,
时, 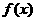 取得最大值
取得最大值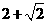 .
.
函数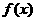 的取得最大值的自变量
的取得最大值的自变量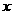 的集合为
的集合为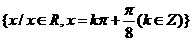 .
.
(II)解:
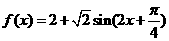
由题意得: 
即: 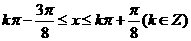
因此函数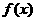 的单调增区间为
的单调增区间为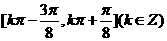 .
.
[点评]本小题考查三角公式,三角函数的性质及已知三角函数值求角等基础知识,考查综合运用三角有关知识的能力.
(18) (本小题满分12分)]
已知正方形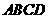 .
.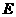 、
、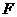 分别是
分别是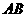 、
、 的中点,将
的中点,将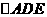 沿
沿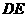 折起,如图所示,记二面角
折起,如图所示,记二面角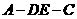 的大小为
的大小为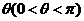 .
.
(I) 证明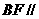 平面
平面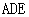 ;
;
(II)若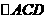 为正三角形,试判断点
为正三角形,试判断点 在平面
在平面 内的射影
内的射影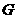 是否在直线
是否在直线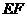 上,证明你的结论,并求角
上,证明你的结论,并求角 的余弦值.
的余弦值.
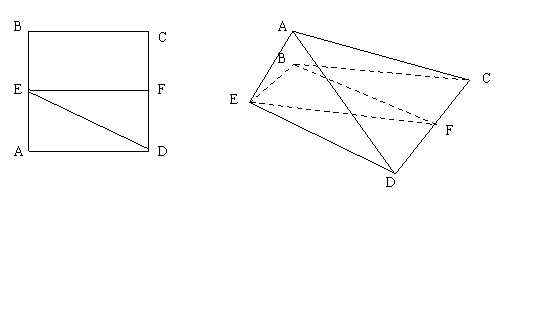

[解析](I)证明:EF分别为正方形ABCD得边AB、CD的中点,
 EB//FD,且EB=FD,
EB//FD,且EB=FD,
 四边形EBFD为平行四边形.
四边形EBFD为平行四边形.
 BF//ED
BF//ED
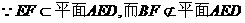

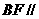 平面
平面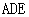 .
.
(II)解法1:
如右图,点A在平面BCDE内的射影G在直线EF上,
过点A作AG垂直于平面BCDE,垂足为G,连结GC,GD.

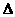 ACD为正三角形,
ACD为正三角形,
 AC=AD
AC=AD
 CG=GD
CG=GD
 G在CD的垂直平分线上,
G在CD的垂直平分线上,
 点A在平面BCDE内的射影G在直线EF上,
点A在平面BCDE内的射影G在直线EF上,
过G作GH垂直于ED于H,连结AH,则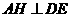 ,所以
,所以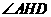 为二面角A-DE-C的平面角.即
为二面角A-DE-C的平面角.即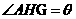
设原正方体的边长为2a,连结AF
在折后图的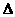 AEF中,AF=
AEF中,AF=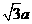 ,EF=2AE=2a,
,EF=2AE=2a,
即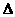 AEF为直角三角形,
AEF为直角三角形, 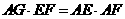
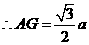
在Rt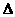 ADE中,
ADE中, 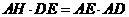
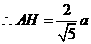
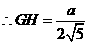
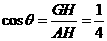 .
.
解法2:点A在平面BCDE内的射影G在直线EF上
连结AF,在平面AEF内过点作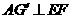 ,垂足为
,垂足为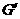 .
.

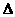 ACD为正三角形,F为CD的中点,
ACD为正三角形,F为CD的中点,
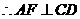
又因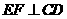 ,
,
所以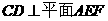

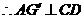
又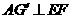 且
且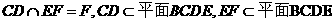
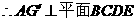
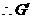 为A在平面BCDE内的射影G.
为A在平面BCDE内的射影G.
即点A在平面BCDE内的射影在直线EF上
过G作GH垂直于ED于H,连结AH,则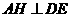 ,所以
,所以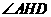 为二面角A-DE-C的平面角.即
为二面角A-DE-C的平面角.即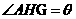
设原正方体的边长为2a,连结AF
在折后图的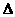 AEF中,AF=
AEF中,AF=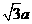 ,EF=2AE=2a,
,EF=2AE=2a,
即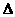 AEF为直角三角形,
AEF为直角三角形, 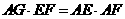
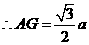
在Rt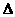 ADE中,
ADE中, 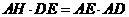
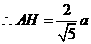
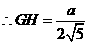
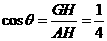 .
.
解法3: 点A在平面BCDE内的射影G在直线EF上
连结AF,在平面AEF内过点作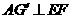 ,垂足为
,垂足为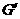 .
.

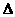 ACD为正三角形,F为CD的中点,
ACD为正三角形,F为CD的中点,
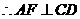
又因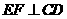 ,
,
所以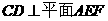
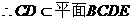
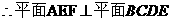
又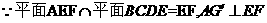
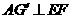
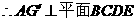
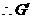 为A在平面BCDE内的射影G.
为A在平面BCDE内的射影G.
即点A在平面BCDE内的射影在直线EF上
过G作GH垂直于ED于H,连结AH,则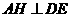 ,所以
,所以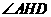 为二面角A-DE-C的平面角.即
为二面角A-DE-C的平面角.即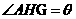
设原正方体的边长为2a,连结AF
在折后图的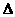 AEF中,AF=
AEF中,AF=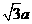 ,EF=2AE=2a,
,EF=2AE=2a,
即 AEF为直角三角形,
AEF为直角三角形, 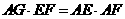
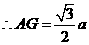
在Rt ADE中,
ADE中, 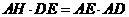
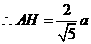
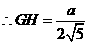 ,
,
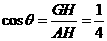 .
.
[点评]本小题考查空间中的线面关系,解三角形等基础知识考查空间想象能力和思维能力.
(19) (本小题满分12分)
现有甲、乙两个项目,对甲项目每投资十万元,一年后利润是1.2万元、1.18万元、1.17万元的概率分别为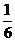 、
、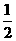 、
、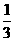 ;已知乙项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是
;已知乙项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是 ,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为
,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为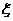 ,对乙项目每投资十万元,
,对乙项目每投资十万元, 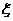 取0、1、2时,
一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量
取0、1、2时,
一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量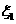 、
、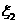 分别表示对甲、乙两项目各投资十万元一年后的利润.
分别表示对甲、乙两项目各投资十万元一年后的利润.
(I) 求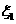 、
、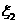 的概率分布和数学期望
的概率分布和数学期望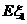 、
、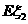 ;
;
(II) 当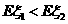 时,求
时,求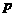 的取值范围.
的取值范围.
[解析]
(I)解法1:
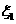 的概率分布为
的概率分布为
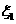 |
1.2 |
1.18 |
1.17 |
|
P |
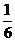 |
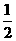 |
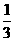 |
E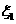 =1.2
=1.2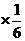 +1.18
+1.18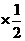 +1.17
+1.17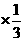 =1.18.
=1.18.
由题设得 ,则
,则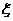 的概率分布为
的概率分布为
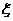 |
0 |
1 |
2 |
|
P |
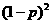 |
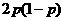 |
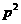 |
故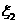 的概率分布为
的概率分布为
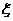 |
1.3 |
1.25 |
0.2 |
|
P |
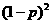 |
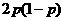 |
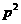 |
所以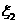 的数学期望为
的数学期望为
E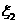 =
=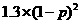 +
+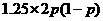 +
+ =
= .
.
解法2: 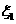 的概率分布为
的概率分布为
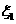 |
1.2 |
1.18 |
1.17 |
|
P |
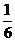 |
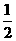 |
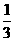 |
E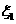 =1.2
=1.2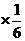 +1.18
+1.18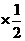 +1.17
+1.17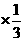 =1.18.
=1.18.
设 表示事件”第i次调整,价格下降”(i=1,2),则
表示事件”第i次调整,价格下降”(i=1,2),则
P(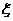 =0)=
=0)= 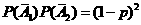 ;
;
P(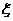 =1)=
=1)=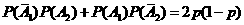 ;
;
P(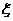 =2)=
=2)=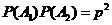
故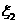 的概率分布为
的概率分布为
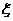 |
1.3 |
1.25 |
0.2 |
|
P |
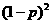 |
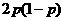 |
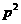 |
所以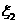 的数学期望为
的数学期望为
E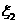 =
=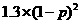 +
+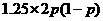 +
+ =
= .
.
(II) 由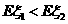 ,得:
,得:
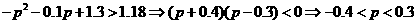
因0<p<1,所以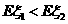 时,p的取值范围是0<p<0.3.
时,p的取值范围是0<p<0.3.
[点评]本小题考查二项分布、分布列、数学期望、方差等基础知识,考查同学们运用概率知识解决实际问题的能力.
(20) (本小题满分14分)
已知点 ,
,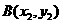
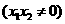 是抛物线
是抛物线 上的两个动点,
上的两个动点, 是坐标原点,向量
是坐标原点,向量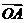 ,
,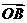 满足
满足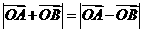 .设圆
.设圆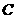 的方程为
的方程为
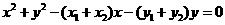
(I) 证明线段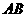 是圆
是圆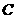 的直径;
的直径;
(II)当圆C的圆心到直线X-2Y=0的距离的最小值为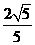 时,求p的值。
时,求p的值。
[解析](I)证明1:
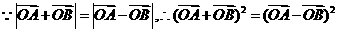
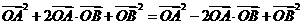
整理得: 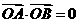
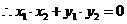
设M(x,y)是以线段AB为直径的圆上的任意一点,则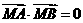
即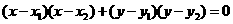
整理得: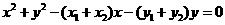
故线段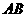 是圆
是圆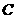 的直径
的直径
证明2: 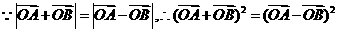
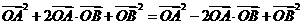
整理得: 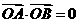
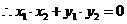 ……..(1)
……..(1)
设(x,y)是以线段AB为直径的圆上则
即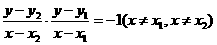
去分母得: 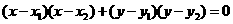
点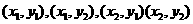 满足上方程,展开并将(1)代入得:
满足上方程,展开并将(1)代入得:
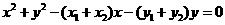
故线段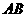 是圆
是圆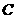 的直径
的直径
证明3: 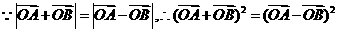
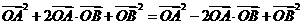
整理得: 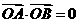
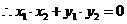 ……(1)
……(1)
以线段AB为直径的圆的方程为

展开并将(1)代入得:
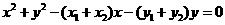
故线段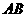 是圆
是圆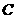 的直径
的直径
(II)解法1:设圆C的圆心为C(x,y),则
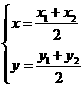
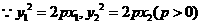
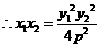
又因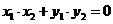
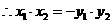
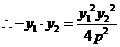
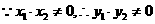
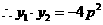
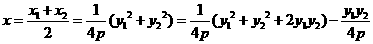
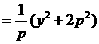
所以圆心的轨迹方程为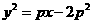
设圆心C到直线x-2y=0的距离为d,则
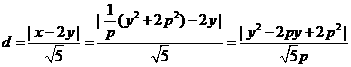
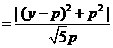
当y=p时,d有最小值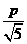 ,由题设得
,由题设得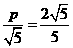
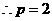 .
.
解法2: 设圆C的圆心为C(x,y),则
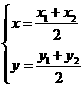
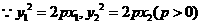
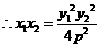
又因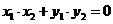
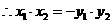
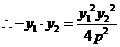
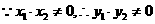
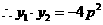
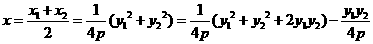
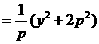
所以圆心的轨迹方程为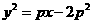
设直线x-2y+m=0到直线x-2y=0的距离为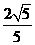 ,则
,则
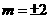
因为x-2y+2=0与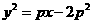 无公共点,
无公共点,
所以当x-2y-2=0与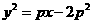 仅有一个公共点时,该点到直线x-2y=0的距离最小值为
仅有一个公共点时,该点到直线x-2y=0的距离最小值为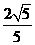
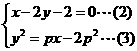
将(2)代入(3)得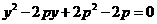

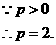
解法3: 设圆C的圆心为C(x,y),则
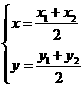
圆心C到直线x-2y=0的距离为d,则
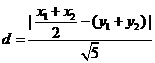
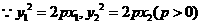
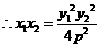
又因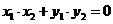
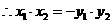
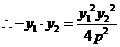
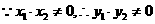
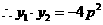
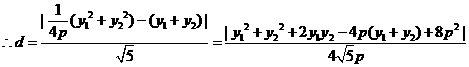
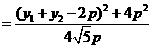
当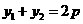 时,d有最小值
时,d有最小值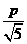 ,由题设得
,由题设得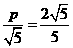
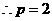 .
.
[点评]本小题考查了平面向量的基本运算,圆与抛物线的方程.点到直线的距离公式等基础知识,以及综合运用解析几何知识解决问题的能力.
21.(本小题满分12分)
已知函数f(x)=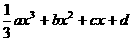 ,其中a , b , c是以d为公差的等差数列,,且a>0,d>0.设
,其中a , b , c是以d为公差的等差数列,,且a>0,d>0.设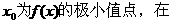 [1-
[1-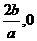 ]上,
]上, ,在
,在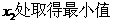 ,将点
,将点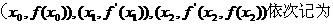 A, B, C
A, B, C
(I)求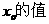
(II)若⊿ABC有一边平行于x轴,且面积为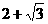 ,求a ,d的值
,求a ,d的值
[解析](I)解:
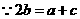
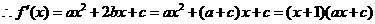
令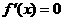 ,得
,得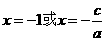
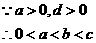
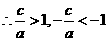
当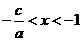 时,
时, 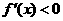 ;
;
当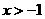 时,
时, 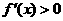
所以f(x)在x=-1处取得最小值即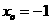
(II) 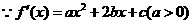
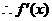 的图像的开口向上,对称轴方程为
的图像的开口向上,对称轴方程为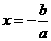
由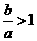 知
知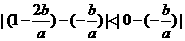
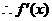 在
在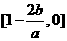 上的最大值为
上的最大值为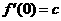
即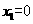
又由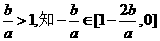
 当
当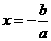 时,
时, 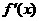 取得最小值为
取得最小值为
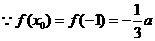
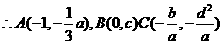
由三角形ABC有一条边平行于x轴知AC平行于x轴,所以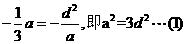
又由三角形ABC的面积为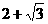 得
得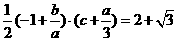
利用b=a+d,c=a+2d,得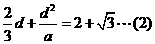
联立(1)(2)可得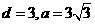 .
.
解法2: 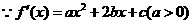
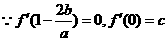
又c>0知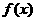 在
在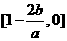 上的最大值为
上的最大值为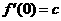
即: 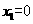
又由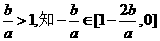
 当
当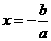 时,
时, 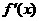 取得最小值为
取得最小值为
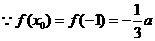
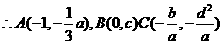
由三角形ABC有一条边平行于x轴知AC平行于x轴,所以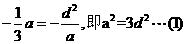
又由三角形ABC的面积为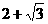 得
得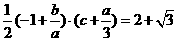
利用b=a+d,c=a+2d,得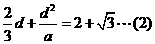
联立(1)(2)可得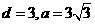
[点评]本小题考查了函数的导数,函数的极值的判定,闭区间上二次函数的最值,等差数基础知识的综合应用,考查了应用数形结合的数学思想分析问题解决问题的能力
(13) 设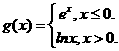 则
则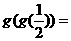 __________
__________
[解析]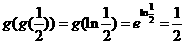 .
.
[点评]本题考察了分段函数的表达式、指对数的运算.
(14) 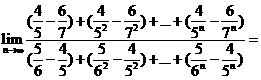 _____________
_____________
[解析]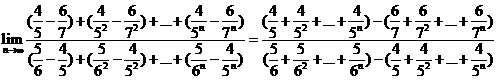

[点评]本题考查了等比数列的求和公式以及数列极限的基本类型.
(15) 5名乒乓球队员中,有2名老队员和3名新队员.现从中选出3名队员排成1、2、3号参加团体比赛,则入选的3名队员中至少有一名老队员,且1、2号中至少有1名新队员的排法有_______种.(以数作答)
[解析]两老一新时, 有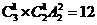 种排法;
种排法;
两新一老时, 有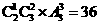 种排法,即共有48种排法.
种排法,即共有48种排法.
[点评]本题考查了有限制条件的排列组合问题以及分类讨论思想.
(16) 若一条直线与一个正四棱柱各个面所成的角都为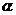 ,则
,则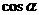 =______
=______
[解析]不妨认为一个正四棱柱为正方体,与正方体的所有面成角相等时,为与相交于同一顶点的三个相互垂直的平面所成角相等,即为体对角线与该正方体所成角.故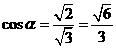 .
.
[点评]本题考查了直线与平面所成角的定义以及正四棱柱的概念,充分考查了转化思想的应用.
22.已知函数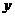 =
= +
+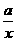 有如下性质:如果常数
有如下性质:如果常数 >0,那么该函数在
>0,那么该函数在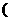 0,
0,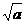
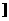 上是减函数,在
上是减函数,在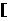
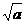 ,+∞
,+∞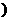 上是增函数.
上是增函数.
(1)如果函数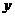 =
= +
+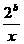 (
( >0)的值域为
>0)的值域为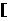 6,+∞
6,+∞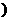 ,求
,求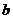 的值;
的值;
(2)研究函数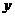 =
=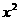 +
+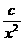 (常数
(常数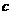 >0)在定义域内的单调性,并说明理由;
>0)在定义域内的单调性,并说明理由;
(3)对函数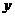 =
= +
+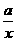 和
和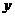 =
=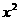 +
+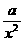 (常数
(常数 >0)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),并求函数
>0)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),并求函数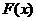 =
=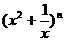 +
+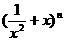 (
(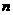 是正整数)在区间[
是正整数)在区间[ ,2]上的最大值和最小值(可利用你的研究结论).
,2]上的最大值和最小值(可利用你的研究结论).
解:(1)易知,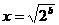 时,
时, 。
。
(2)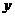 =
=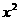 +
+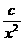 是偶函数。易知,该函数在
是偶函数。易知,该函数在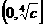 上是减函数,在
上是减函数,在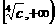 上是增函数;则该函数在
上是增函数;则该函数在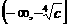 上是减函数,在
上是减函数,在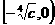 上是增函数。
上是增函数。
(3)推广:函数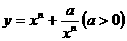 ,当
,当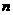 为奇数时,
为奇数时,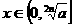 ,
,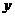 是减函数;
是减函数;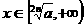 ,
,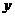 是增函数。
是增函数。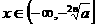 ,
,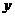 是增函数;
是增函数;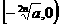 ,
,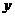 是减函数。
是减函数。
当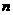 为偶数时,
为偶数时,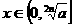 ,
,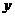 是减函数;
是减函数;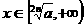 ,
,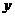 是增函数。
是增函数。
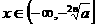 ,
,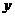 是减函数;
是减函数;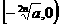 ,
,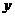 是增函数。
是增函数。
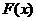 =
=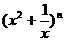 +
+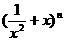
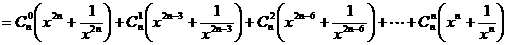
当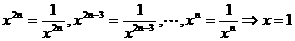 时,
时,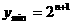 。
。
∴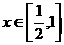 ,
,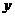 是减函数;
是减函数;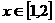 ,
,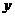 是增函数。
是增函数。
∵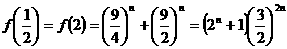
∴函数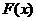 =
=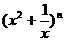 +
+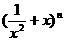 在区间[
在区间[ ,2]上的最大值为
,2]上的最大值为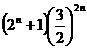 ,最小值为
,最小值为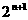 。
。
21.已知有穷数列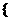
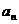
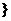 共有2
共有2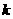 项(整数
项(整数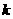 ≥2),首项
≥2),首项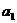 =2.设该数列的前
=2.设该数列的前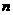 项和为
项和为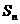 ,且
,且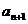 =
=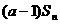 +2(
+2(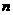 =1,2,┅,2
=1,2,┅,2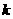 -1),其中常数
-1),其中常数 >1.
>1.
(1)求证:数列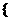
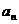
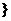 是等比数列;
是等比数列;
(2)若 =2
=2 ,数列
,数列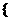
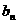
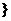 满足
满足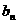 =
=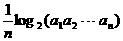 (
(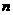 =1,2,┅,2
=1,2,┅,2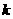 ),求数列
),求数列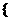
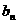
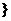 的通项公式;
的通项公式;
(3)若(2)中的数列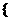
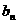
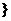 满足不等式|
满足不等式|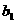 -
-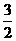 |+|
|+|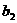 -
-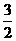 |+┅+|
|+┅+|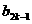 -
-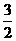 |+|
|+|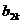 -
-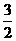 |≤4,求
|≤4,求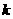 的值.
的值.
解:(1)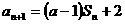 ,则
,则 ,两式相减,得
,两式相减,得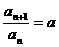 ,
,
(又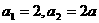 )
)
∴数列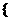
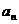
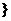 是首项为
是首项为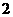 、公比为
、公比为 的等比数列。
的等比数列。
(2)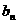 =
=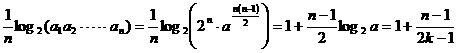 ,(
,(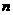 =1,2,┅,2
=1,2,┅,2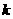 )。
)。
(3)由(2)知,数列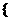
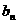
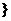 是首项为
是首项为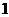 、公差为
、公差为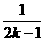 的等差数列。
的等差数列。
又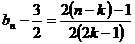 ,∴
,∴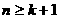 时,
时,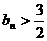 ;
; 时,
时,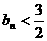 。
。
∴|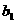 -
-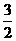 |+|
|+|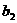 -
-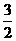 |+┅+|
|+┅+|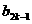 -
-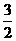 |+|
|+|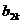 -
-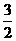 |
|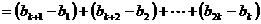
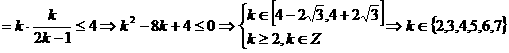 。
。
20、在平面直角坐标系 O
O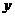 中,直线
中,直线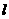 与抛物线
与抛物线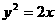 相交于
相交于 、
、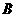 两点。
两点。
(1)求证:“如果直线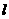 过点
过点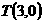 ,那么
,那么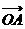
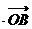 =
= ”是真命题;
”是真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由。
解:(1)如果直线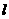
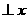 轴,则
轴,则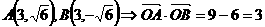
如果直线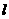 与
与 轴不垂直,设直线
轴不垂直,设直线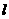 的方程为
的方程为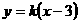 ,
,
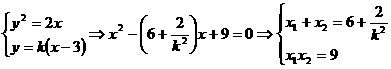
∴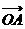
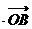
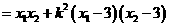

综上,得“如果直线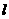 过点
过点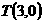 ,那么
,那么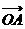
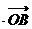 =
= ”是真命题。
”是真命题。
(2)(1)中命题的逆命题:在平面直角坐标系 O
O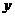 中,直线
中,直线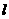 与抛物线
与抛物线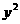 =2
=2 相交于
相交于 、
、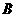 两点。如果
两点。如果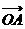
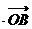 =
= ,那么直线
,那么直线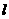 必过点
必过点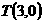 。
。
∵设直线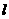 与
与 轴的交点坐标为
轴的交点坐标为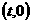 ,则直线方程为
,则直线方程为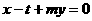 ,把它代入
,把它代入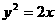 得
得
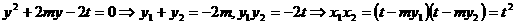
由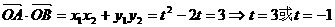 ,即直线
,即直线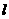 必过点
必过点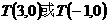 。
。
∴(1)中命题的逆命题是假命题。
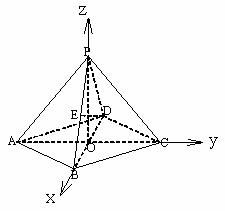
19、在四棱锥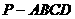 中,底面是边长为
中,底面是边长为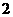 的菱形,
的菱形,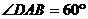 ,对角线
,对角线 与
与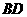 相交于点
相交于点 ,
,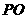 ⊥平面
⊥平面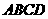 ,
,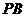 与平面
与平面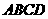 所成的角为
所成的角为 .
.
(1)求四棱锥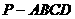 的体积;
的体积;
(2)若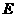 是
是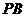 的中点,求异面直线
的中点,求异面直线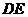 与
与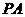 所成角的大小(结果用反三角函数值表示).
所成角的大小(结果用反三角函数值表示).
解:(1)底面是边长为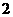 的菱形,
的菱形,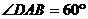
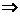
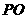 ⊥平面
⊥平面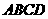 ,
,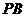 与平面
与平面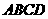 所成的角为
所成的角为
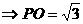 ,
,
∴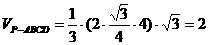 。
。
(2)建系如图,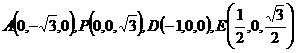 ,
,
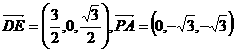 ,
,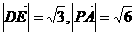 ,
,
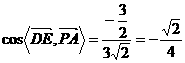 ,
,
∴异面直线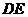 与
与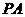 所成角的大小为
所成角的大小为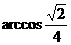 。
。
18、如图,当甲船位于 处时获悉,在其正东方向相距
处时获悉,在其正东方向相距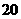 海里的
海里的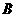 处有一艘渔船遇险等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西
处有一艘渔船遇险等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西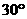 ,相距
,相距 海里
海里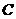 处的乙船,试问乙船应朝北偏东多少度的方向沿直线前往
处的乙船,试问乙船应朝北偏东多少度的方向沿直线前往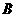 处救援(角度精确到
处救援(角度精确到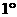 )?
)?
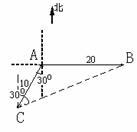 解:
解: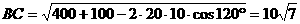
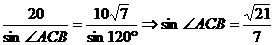
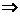
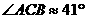
∴乙船应朝北偏东约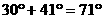 的方向沿直线前往
的方向沿直线前往 处救援。
处救援。
16、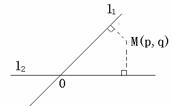 如图,平面中两条直线
如图,平面中两条直线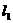 和
和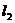 相交于点
相交于点 。对于平面上任意一点
。对于平面上任意一点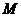 ,若
,若 、
、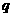 分别是
分别是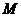 到直线
到直线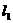 和
和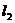 的距离,则称有序非负实数对
的距离,则称有序非负实数对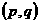 是点
是点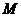 的“距离坐标”。已知常数
的“距离坐标”。已知常数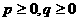 ,给出下列三个命题:
,给出下列三个命题:
①若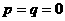 ,则“距离坐标”为
,则“距离坐标”为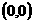 的点有且仅有1个。
的点有且仅有1个。
②若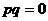 ,且
,且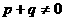 ,则“距离坐标”为
,则“距离坐标”为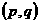 的点有且仅有2个。
的点有且仅有2个。
③若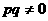 ,则“距离坐标”为
,则“距离坐标”为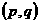 的点有且仅有4个。
的点有且仅有4个。
上述命题中,正确命题的个数是 ( D )
(A)0 (B)1 (C)2 (D)3

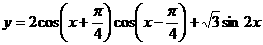 的值域和最小正周期。
的值域和最小正周期。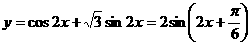 ,
,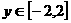 ,
,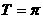 。
。 的不等式
的不等式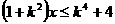 的解集是
的解集是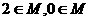 (B)
(B)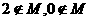 (C)
(C)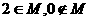 (D)
(D)