不等式解法,包括一元一次不等式(组)、一元二次不等式(组)、分式不等式、高次不等式等有理不等式,简单的无理不等式、指数不等式、对数不等式以及含有绝对值符号的不等式的求解和解集的确定.
1、形如ax+b>0和ax2+bx+c>0(<0)(a¹0)的不等式(组)的解法和解集的确定要熟练掌握.它们是解各种类型不等式的基础.高次不等式的解法是通过因式分解,将它化为一次或二次因式的乘积,然后用“序轴标根法”求解集.解有理分式不等式时,一般先通过移项,把一边化为零,另一边化为因式之积或商,再等价转化为高次不等式解之.
(1)若a>b>c,则一定成立的不等式是( ).
(A)a|c|>b|c| (B)ab>ac
(C)a-|c|>b-|c| (D)a-|c|<b-|c|
(2)若x<a<0,则一定成立的不等式是( ).
(A)x2<ax<a2 (B)x2>ax>a2
(C)x2<a2<ax (D)x2>a2>ax
(3)a,bÎR,下列命题中的真命题是( ).
(A)若a>b,则|a|>|b| (B)若a>b,则
(C)若a>b,则a3>b3
(D)若a>b,则
(4)设a,b是满足ab<0的实数,则( ).
(A)|a+b|<|a-b| (B)|a+b|>|a-b|
(C)|a-b|<||a|-|b|| (D)|a-b|<|a|+|b|
(5)以下四个不等式:¬a<0<b;b<a<0;® b<0<a;¯0<b<a,其中使 成立的充分条件有( ).
成立的充分条件有( ).
(A)1个 (B)2个 (C)3个 (D)4个
(6)已知a<b,化简|a-b-3|-|b-a+2|=_______
(7)已知a>b>c>d>0,且 则e,f的大小关系是_____________
则e,f的大小关系是_____________
(8)已知 ,则a,b,0,1的大小顺序是________
,则a,b,0,1的大小顺序是________
(9)x>y或 同时成立的充要条件是_______________
同时成立的充要条件是_______________
(10)已知a,b为不等正数,s<t<0,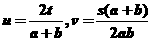 则u,v的大小关系是 ________________
则u,v的大小关系是 ________________
(11)已知-1<2a<0,将下列各数按照从小到大的顺序排列,并说明理由.
(12)已知a为正数, ,试比较
,试比较 四个数的大小.
四个数的大小.
第二节 不等式的解法
例1 若a,b是任意实数,且a>b,则( ).
(A)a2>b2 (B)<1 (C)lg(a-b)>0 (D)
例2 已知都是实数,给出下列命题;
①ac2>bc2Ûa>b
②
③(x-a)(x-b)£0Û
 ④
④
其中正确命题的个数是( ).
(A)1 (B)2 (C)3 (D)4
例3 设a,b是不相等的正数,  ,
,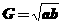 ,
, ,
, .试比较A、G、H、Q的大小.
.试比较A、G、H、Q的大小.
例4 船在流水中在甲地和乙地间来回行驶一次的平均速度和船在静水中的速度是否相等,为什么?
2、不等式的性质包括基本性质和运算性质两部分
(1)基本性质:a>bÛb>a;
a>b,b>cÛa>c;
a>bÛa+c>b+c;
c>0时,a>bÛac>bc;
c<0时,a>bÛac<bc.
(2)运算性质:a>b,c>dÞa+c>b+d;
a>b,c<dÞa-c>b-d;
a>b>0,c>d>0Þac>bd;
a>b>0,c>d>0Þ>
a>b>0Þan>bn (nÎN且n>1);
a>b>0Þ > (nÎN且n>1).
上述性质中,条件与结论的逻辑关系有两种:推出关系“Þ”和等价关系“Û”,要注意区别.一般地,证明不等式时,进行的是一系列推出变换;解不等式时,进行的是一系列等价变换.不等式的概念和性质是进行变换、证明不等式和解不等式的依据.

 ,定义函数
,定义函数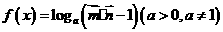 ,求函数
,求函数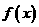 的最小正周期、单调递增区间。
的最小正周期、单调递增区间。 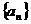 的公差
的公差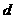 大于0,且
大于0,且 、
、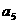 是方程
是方程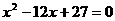 的两根,数列
的两根,数列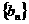 的前
的前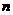 项和为
项和为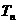 ,且
,且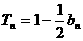
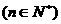 。求数列
。求数列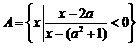 ,
, ,若
,若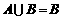 ,求实数
,求实数 的取值范围。
的取值范围。 满足
满足 ,
,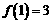 ,则
,则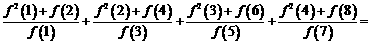 ____ ___.
____ ___.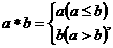 例如,
例如,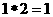 ,则函数f(x)=
,则函数f(x)= 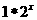 的值域为 .
的值域为 .