21.已知有穷数列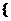
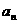
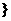 共有2
共有2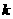 项(整数
项(整数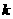 ≥2),首项
≥2),首项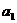 =2.设该数列的前
=2.设该数列的前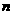 项和为
项和为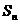 ,且
,且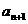 =
=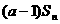 +2(
+2(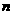 =1,2,┅,2
=1,2,┅,2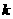 -1),其中常数
-1),其中常数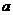 >1.
>1.
(1)求证:数列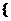
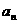
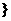 是等比数列;
是等比数列;
(2)若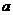 =2
=2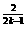 ,数列
,数列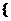
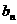
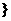 满足
满足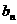 =
=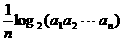 (
(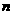 =1,2,┅,2
=1,2,┅,2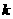 ),求数列
),求数列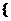
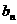
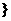 的通项公式;
的通项公式;
(3)若(2)中的数列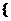
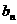
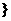 满足不等式|
满足不等式|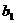 -
-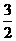 |+|
|+|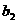 -
-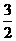 |+┅+|
|+┅+|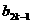 -
-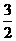 |+|
|+|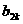 -
-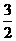 |≤4,求
|≤4,求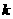 的值.
的值.
解:(1)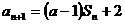 ,则
,则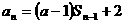 ,两式相减,得
,两式相减,得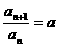 ,
,
(又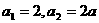 )
)
∴数列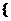
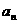
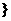 是首项为
是首项为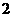 、公比为
、公比为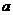 的等比数列。
的等比数列。
(2)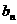 =
=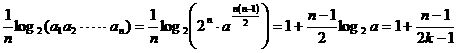 ,(
,(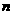 =1,2,┅,2
=1,2,┅,2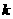 )。
)。
(3)由(2)知,数列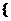
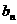
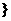 是首项为
是首项为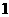 、公差为
、公差为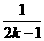 的等差数列。
的等差数列。
又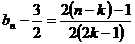 ,∴
,∴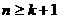 时,
时,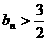 ;
;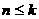 时,
时,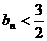 。
。
∴|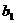 -
-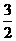 |+|
|+|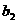 -
-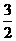 |+┅+|
|+┅+|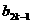 -
-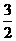 |+|
|+|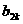 -
-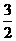 |
|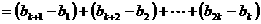
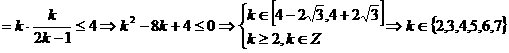 。
。
- 答案

