22.(重庆卷)将5名实习教师分配到高一年级的3个班实习,每班至少1名,最多2名,则不同的分配方案有
(A)30种 (B)90种 (C)180种 (D)270种
解析:将5名实习教师分配到高一年级的3个班实习,每班至少1名,最多2名,则将5名教师分成三组,一组1人,另两组都是2人,有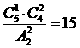 种方法,再将3组分到3个班,共有
种方法,再将3组分到3个班,共有 种不同的分配方案,选B.
种不同的分配方案,选B.
21.(重庆卷)若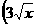 -
-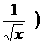 n的展开式中各项系数之和为64,则展开式的常数项为
n的展开式中各项系数之和为64,则展开式的常数项为
(A)-540 (B)-162 (C)162 (D)540
解析:若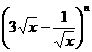 的展开式中各项系数之和为
的展开式中各项系数之和为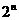 =64,
=64,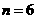 ,则展开式的常数项为
,则展开式的常数项为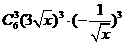 =-540,选A.
=-540,选A.
19.(浙江卷)函数f:|1,2,3|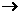 |1,2,3|满足f(f(x))=
f(x),则这样的函数个数共有
|1,2,3|满足f(f(x))=
f(x),则这样的函数个数共有
(A)1个 (B)4个 (C)8个 (D)10个
[考点分析]本题考查抽象函数的定义,中档题。
解析: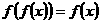 即
即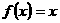
20(浙江卷)在二项式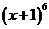 的展开式中,含
的展开式中,含 的项的系数是
的项的系数是
(A)15 (B)20 (C)30 (D)40
解析:含 的项的系数是
的项的系数是
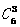 =20,选B
=20,选B
18.(浙江卷)若多项式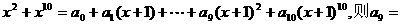
(A)9 (B)10 (C)-9 (D)-10
[考点分析]本题考查二项式展开式的特殊值法,基础题。
解析:令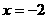 ,得
,得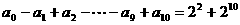 ,
,
令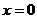 ,得
,得
17.(天津卷)将4个颜色互不相同的球全部放入编号为1和2的两个盒子里,使得放入每个盒子里的球的个数不小于该盒子的编号,则不同的放球方法有( )
A.10种 B.20种 C.36种 D.52种
解析:将4个颜色互不相同的球全部放入编号为1和2的两个盒子里,使得放入每个盒子里的球的个数不小于该盒子的编号,分情况讨论:①1号盒子中放1个球,其余3个放入2号盒子,有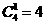 种方法;②1号盒子中放2个球,其余2个放入2号盒子,有
种方法;②1号盒子中放2个球,其余2个放入2号盒子,有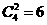 种方法;则不同的放球方法有10种,选A.
种方法;则不同的放球方法有10种,选A.
16.(山东卷)已知( )
) 的展开式中第三项与第五项的系数之比为
的展开式中第三项与第五项的系数之比为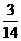 ,则展开式中常数项是
,则展开式中常数项是
(A)-1 (B)1 (C)-45 (D)45
解:第三项的系数为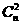 ,第五项的系数为
,第五项的系数为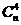 ,由第三项与第五项的系数之比为
,由第三项与第五项的系数之比为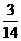 可得n=10,则
可得n=10,则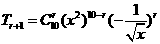 =
=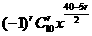 ,令40-5r=0,解得r=8,故所求的常数项为
,令40-5r=0,解得r=8,故所求的常数项为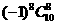 =45,选D
=45,选D
15.(山东卷)已知 的展开式中第三项与第五项的系数之比为-
的展开式中第三项与第五项的系数之比为-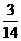 ,其中
,其中 =-1,则展开式中常数项是
=-1,则展开式中常数项是
(A)-45i (B) 45i (C) -45 (D)45
解:第三项的系数为-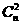 ,第五项的系数为
,第五项的系数为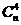 ,由第三项与第五项的系数之比为-
,由第三项与第五项的系数之比为-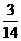 可得n=10,则
可得n=10,则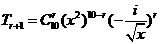 =
=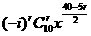 ,令40-5r=0,解得r=8,故所求的常数项为
,令40-5r=0,解得r=8,故所求的常数项为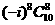 =45,选A
=45,选A
14.(山东卷)已知集合A={5},B={1,2},C={1,3,4},从这三个集合中各取一个元素构成空间直角坐标系中点的坐标,则确定的不同点的个数为
(A)33 (B) 34 (C) 35 (D)36
解:不考虑限定条件确定的不同点的个数为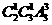 =36,但集合B、C中有相同元素1,由5,1,1三个数确定的不同点的个数只有三个,故所求的个数为36-3=33个,选A
=36,但集合B、C中有相同元素1,由5,1,1三个数确定的不同点的个数只有三个,故所求的个数为36-3=33个,选A
13.(全国II)5名志愿者分到3所学校支教,每个学校至少去一名志愿者,则不同的分派方法共有
(A)150种 (B)180种 (C)200种 (D)280种
解:人数分配上有1,2,2与1,1,3两种方式,若是1,2,2,则有 =60种,若是1,1,3,则有
=60种,若是1,1,3,则有 =90种,所以共有150种,选A
=90种,所以共有150种,选A

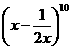 的展开式中,
的展开式中,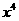 的系数为
的系数为 B.
B.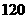 C.
C.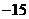 D.
D.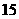
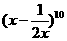 的展开式中,x4项是
的展开式中,x4项是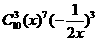 =-15x4,选C.
=-15x4,选C.