18．(上海卷)在一个小组中有8名女同学和4名男同学，从中任意地挑选2名同学担任交通安全宣传志愿者，那么选到的两名都是女同学的概率是______(结果用分数表示)。

解：在一个小组中有8名女同学和4名男同学，从中任意地挑选2名同学担任交通安全宣传志愿者，那么选到的两名都是女同学的概率是.

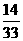17．(上海卷)两部不同的长篇小说各由第一、二、三、四卷组成，每卷1本，共8本．将它们任意地排成一排，左边4本恰好都属于同一部小说的概率是 　　　　　　　(结果用分数表示)．

解：分为二步完成： 1) 两套中任取一套，再作全排列，有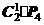种方法；2) 剩下的一套全排列，有种方法；所以，所求概率为：；

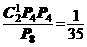16．(山东卷)某学校共有师生2400人，现用分层抽样的方法，从所有师生中抽取一个容量为160的样本，已知从学生中抽取的人数为150，那么该学校的教师人数是　　　.

解：抽取教师为160-150=10人，所以学校教师人数为2400×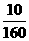=150 人。

15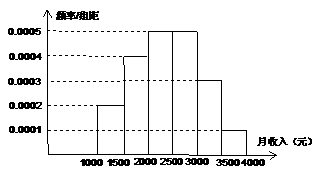．(全国II)一个社会调查机构就某地居民

的月收入调查了10 000人，并根据所得数据画了

样本的频率分布直方图(如右图)．为了分析居

民的收入与年龄、学历、职业等方面的关系，要

从这10 000人中再用分层抽样方法抽出100人作

进一步调查，则在［2500，3000)(元)月收入

段应抽出　　　　　　　 人．

解析:由直方图可得(元)月收入段共有人

按分层抽样应抽出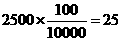人

14．(湖南卷)某高校有甲、乙两个数学建模兴趣班. 其中甲班有40人，乙班50人. 现分析两个班的一次考试成绩，算得甲班的平均成绩是90分，乙班的平均成绩是81分，则该校数学建模兴趣班的平均成绩是　　　分.

解析：某高校有甲、乙两个数学建模兴趣班. 其中甲班有40人，乙班50人. 现分析两个班的一次考试成绩，算得甲班的平均成绩是90分，乙班的平均成绩是81分，则该校数学建模兴趣班的平均成绩是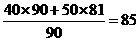分.

13．(湖北卷)接种某疫苗后，出现发热反应的概率为0．80，现有5人接种了该疫苗，至少有3人出现发热反应的概率为　　　　　 。(精确到0．01)

解：P＝＝0.94

12．(福建卷)一个均匀小正方体的六个面中，三个面上标以数0，两个面上标以数1,一个面上标以数2，将这个小正方体抛掷2次，则向上的数之积的数学期望是　　　　　　　　

解析：一个均匀小正方体的6个面中，三个面上标以数0，两个面上标以数1，一个面上标以数2。将这个小正方体抛掷2次，向上的数之积可能为ξ=0，1，2，4，则，，，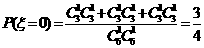

，∴ .

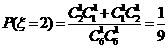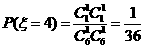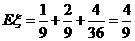11．(重庆卷)某地区有300家商店，其中大型商店有30家 ，中型商店有75家，小型商店有195家。为了掌握各商店的营业情况，要从中抽取一个容量为20的样本。若采用分层抽样的方法，抽取的中型商店数是

(A)2　　 　　　　(B)3　　 　　　(C)5　　 　　　　(D)13

解：各层次之比为：30:75:195＝2:5:13，所抽取的中型商店数是5，故选C

10．(重庆卷)为了了解某地区高三学生的身体发育情况，抽查了该地区100名年龄为17.5岁－18岁的男生体重(kg) ,得到频率分布直方图如下：

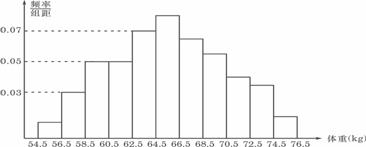
根据上图可得这100名学生中体重在(56.5,64.5)的学生人数是

(A)20　　　　　　 (B)30　　　　　　　 (C)40　　　　　　　 (D)50

解析：根据该图可知，组距为2，得这100名学生中体重在的学生人数所占的频率为(0.03+0.05+0.05+0.07)×2=0.4，所以该段学生的人数是40，选C.

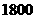9．(四川卷)甲校有名学生，乙校有名学生，丙校有名学生，为统计三校学生某方面的情况，计划采用分层抽样法，抽取一个容量为人的样本，应在这三校分别抽取学生

(A)人，人，人　　　　　　　　　 (B)人，人，人　

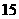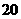(C)人，人，人　　　　　　　　　 (D)人，人，人　

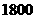解析：甲校有名学生，乙校有名学生，丙校有名学生，为统计三校学生某方面的情况，计划采用分层抽样法，抽取一个容量为人的样本，应在这三校分别抽取学生人，人，人，选B.