28.(湖北卷)某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多参加了其中一组。在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%。登山组的职工占参加活动总人数的 ,且该组中,青年人占50%,中年人占40%,老年人占10%。为了了解各组不同的年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本。试确定
,且该组中,青年人占50%,中年人占40%,老年人占10%。为了了解各组不同的年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本。试确定
(Ⅰ)游泳组中,青年人、中年人、老年人分别所占的比例;
(Ⅱ)游泳组中,青年人、中年人、老年人分别应抽取的人数。
本小题主要考查分层抽样的概念和运算,以及运用统计知识解决实际问题的能力。
解:(Ⅰ)设登山组人数为 ,游泳组中,青年人、中年人、老年人各占比例分别为a、b、c,则有
,游泳组中,青年人、中年人、老年人各占比例分别为a、b、c,则有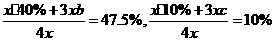 ,解得b=50%,c=10%.
,解得b=50%,c=10%.
故a=100%-50%-10%=40%,即游泳组中,青年人、中年人、老年人各占比例分别为40%、
50%、10%。
(Ⅱ)游泳组中,抽取的青年人数为 (人);抽取的中年人数为
(人);抽取的中年人数为
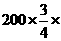 50%=75(人);抽取的老年人数为
50%=75(人);抽取的老年人数为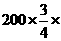 10%=15(人)。
10%=15(人)。
27.(湖北卷)在某校举行的数学竞赛中,全体参赛学生的竞赛成绩近似服从正态分布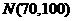 。已知成绩在90分以上(含90分)的学生有12名。
。已知成绩在90分以上(含90分)的学生有12名。
(Ⅰ)、试问此次参赛学生总数约为多少人?
(Ⅱ)、若该校计划奖励竞赛成绩排在前50名的学生,试问设奖的分数线约为多少分?
可共查阅的(部分)标准正态分布表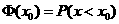
 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1.2 1.3 1.4 1.9 2.0 2.1 |
0.8849 0.9032 0.9192 0.9713 0.9772 0.9821 |
0.8869 0.9049 0.9207 0.9719 0.9778 0.9826 |
0.888 0.9066 0.9222 0.9726 0.9783 0.9830 |
0.8907 0.9082 0.9236 0.9732 0.9788 0.9834 |
0.8925 0.9099 0.9251 0.9738 0.9793 0.9838 |
0.8944 0.9115 0.9265 0.9744 0.9798 0.9842 |
0.8962 0.9131 0.9278 0.9750 0.9803 0.9846 |
0.8980 0.9147 0.9292 0.9756 0.9808 0.9850 |
0.8997 0.9162 0.9306 0.9762 0.9812 0.9854 |
0.9015 0.9177 0.9319 0.9767 0.9817 0.9857 |
点评:本小题主要考查正态分布,对独立事件的概念和标准正态分布的查阅,考查运用概率统计知识解决实际问题的能力。
解:(Ⅰ)设参赛学生的分数为 ,因为
,因为 -N(70,100),由条件知,
-N(70,100),由条件知,
P( ≥90)=1-P(
≥90)=1-P( <90)=1-F(90)=1-
<90)=1-F(90)=1-
 =1-
=1- (2)=1-0.9772=0.228.
(2)=1-0.9772=0.228.
这说明成绩在90分以上(含90分)的学生人数约占全体参赛人数的2.28%,因此,
参赛总人数约为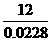 ≈526(人)。
≈526(人)。
(Ⅱ)假定设奖的分数线为x分,则P( ≥x)=1-P(
≥x)=1-P( <x)=1-F(90)=1-
<x)=1-F(90)=1-
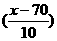 =
=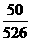 =0.0951,即
=0.0951,即
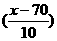 =0.9049,查表得
=0.9049,查表得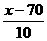 ≈1.31,解得x=83.1.
≈1.31,解得x=83.1.
故设奖得分数线约为83.1分。
26.(广东卷)某运动员射击一次所得环数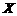 的分布如下:
的分布如下:
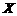 |
6 |
7 |
8 |
9 |
10 |
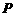 |
0 |
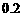 |
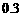 |
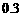 |
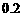 |
现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为 .
.
(I)求该运动员两次都命中7环的概率
(II)求 的分布列
的分布列
解:(Ⅰ)求该运动员两次都命中7环的概率为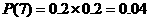 ;
;
(Ⅱ)
 的可能取值为7、8、9、10
的可能取值为7、8、9、10
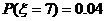



 分布列为
分布列为
 |
7 |
8 |
9 |
10 |
|
P |
0.04 |
0.21 |
0.39 |
0.36 |
(Ⅲ)  的数学希望为
的数学希望为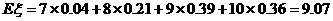 .
.
25.(福建卷)每次抛掷一枚骰子(六个面上分别标以数字
(I)连续抛掷2次,求向上的数不同的概率;
(II)连续抛掷2次,求向上的数之和为6的概率;
(III)连续抛掷5次,求向上的数为奇数恰好出现3次的概率。
本小题主要考查概率的基本知识,运用数学知识解决实际问题的能力。满分12分。
解:(I)设A表示事件“抛掷2次,向上的数不同”,则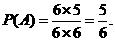
答:抛掷2次,向上的数不同的概率为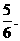
(II)设B表示事件“抛掷2次,向上的数之和为6”。
 向上的数之和为6的结果有
向上的数之和为6的结果有 、
、 、
、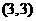 、
、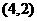 、
、 5种,
5种,
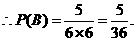
答:抛掷2次,向上的数之和为6的概率为
24.(北京卷)某公司招聘员工,指定三门考试课程,有两种考试方案.
方案一:考试三门课程,至少有两门及格为考试通过;
方案二:在三门课程中,随机选取两门,这两门都及格为考试通过.
假设某应聘者对三门指定课程考试及格的概率分别是0.5,0.6,0.9,且三门课程考试是否及格相互之间没有影响.求:
(Ⅰ)该应聘者用方案一考试通过的概率;
(Ⅱ)该应聘者用方案二考试通过的概率.
解:记该应聘者对三门指定课程考试及格的事件分别为A,B,C,
则P(A)=0.5,P(B)=0.6,P(C)=0.9.
(Ⅰ) 应聘者用方案一考试通过的概率
p1=P(A·B·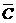 )+P(
)+P(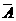 ·B·C)+P(A·
·B·C)+P(A· ·C)+P(A·B·C)
·C)+P(A·B·C)
=0.5×0.6×0.1+0.5×0.6×0.9+0.5×0.4×0.9+0.5×0.6×0.9
=0.03+0.27+0.18+0.27=0.75.
(Ⅱ) 应聘者用方案二考试通过的概率
p2=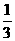 P(A·B)+
P(A·B)+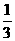 P(B·C)+
P(B·C)+ 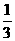 P(A·C)
P(A·C)
=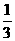 ×(0.5×0.6+0.6×0.9+0.5×0.9)=
×(0.5×0.6+0.6×0.9+0.5×0.9)=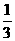 ×1.29=0.43
×1.29=0.43
23.(北京卷)某公司招聘员工,指定三门考试课程,有两种考试方案.
方案一:考试三门课程,至少有两门及格为考试通过;
方案二:在三门课程中,随机选取两门,这两门都及格为考试通过.
假设某应聘者对三门指定课程考试及格的概率分别是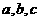 ,且三门课程考试是否及格相互之间没有影响.
,且三门课程考试是否及格相互之间没有影响.
(Ⅰ)分别求该应聘者用方案一和方案二时考试通过的概率;
(Ⅱ)试比较该应聘者在上述两种方案下考试通过的概率的大小.(说明理由)
解:设三门考试课程考试通过的事件分别为A,B,C,相应的概率为a,b,c
(1)考试三门课程,至少有两门及格的事件可表示为AB +A
+A C+
C+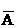 BC+ABC,设其概率为P1,则P1=ab(1-c)+a(1-b)c+(1-a)bc+abc=ab+ac+bc-2abc
BC+ABC,设其概率为P1,则P1=ab(1-c)+a(1-b)c+(1-a)bc+abc=ab+ac+bc-2abc
设在三门课程中,随机选取两门,这两门都及格的概率为P2,则P2=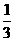 ab+
ab+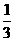 ac+
ac+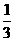 bc
bc
(2)P1-P2=(ab+ac+bc-2abc)-(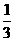 ab+
ab+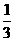 ac+
ac+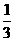 bc)=
bc)= ab+
ab+ ac+
ac+ bc-2abc
bc-2abc
= (ab+ac+bc-3abc)=
(ab+ac+bc-3abc)= (ab(1-c)+ac(1-b)+bc(1-a))>0
(ab(1-c)+ac(1-b)+bc(1-a))>0
\P1>P2即用方案一的概率大于用方案二的概率.
22.(安徽卷)在添加剂的搭配使用中,为了找到最佳的搭配方案,需要对各种不同的搭配方式作比较。在试制某种牙膏新品种时,需要选用两种不同的添加剂。现有芳香度分别为0,1,2,3,4,5的六种添加剂可供选用。根据试验设计原理,通常首先要随机选取两种不同的添加剂进行搭配试验。
(Ⅰ)求所选用的两种不同的添加剂的芳香度之和等于4的概率;
(Ⅱ)求所选用的两种不同的添加剂的芳香度之和不小于3的概率;
解:设“所选用的两种不同的添加剂的芳香度之和等于4”的事件为A,“所选用的两种不同的添加剂的芳香度之和不小于3”的事件为B
(Ⅰ)芳香度之和等于4的取法有2种: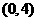 、
、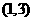 ,故
,故 。
。
(Ⅱ)芳香度之和等于1的取法有1种: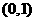 ;芳香度之和等于2的取法有1种:
;芳香度之和等于2的取法有1种: ,故
,故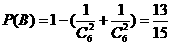 。
。
21.(安徽卷)在添加剂的搭配使用中,为了找到最佳的搭配方案,需要对各种不同的搭配方式作比较。在试制某种牙膏新品种时,需要选用两种不同的添加剂。现有芳香度分别为0,1,2,3,4,5的六种添加剂可供选用。根据试验设计原理,通常首先要随机选取两种不同的添加剂进行搭配试验。用 表示所选用的两种不同的添加剂的芳香度之和。
表示所选用的两种不同的添加剂的芳香度之和。
(Ⅰ)写出 的分布列;(以列表的形式给出结论,不必写计算过程)
的分布列;(以列表的形式给出结论,不必写计算过程)
(Ⅱ)求 的数学期望
的数学期望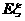 。(要求写出计算过程或说明道理)
。(要求写出计算过程或说明道理)
解:(Ⅰ)
 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
P |
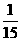 |
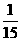 |
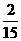 |
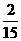 |
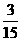 |
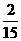 |
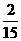 |
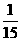 |
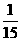 |
(Ⅱ)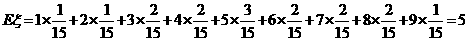
20.(上海春)同学们都知道,在一次考试后,如果按顺序去掉一些高分,那么班级的平均分将降低;反之,如果按顺序去掉一些低分,那么班级的平均分将提高. 这两个事实可以用数学语言描述为:若有限数列 满足
满足 ,则
,则
(结论用数学式子表示).
解:如果在有限数列  中,按顺序去掉一些高分
中,按顺序去掉一些高分  ,那么有不等关系
,那么有不等关系 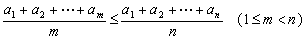 ; 如果在有限数列
; 如果在有限数列  中,按顺序去掉一些低分
中,按顺序去掉一些低分  ,那么有不等关系
,那么有不等关系 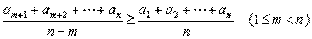 .从而应填
.从而应填
 ,与
,与 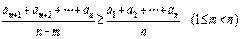 .
三、解答题(共27题)
.
三、解答题(共27题)
19.(四川卷)设离散型随机变量 可能取的值为1,2,3,4。
可能取的值为1,2,3,4。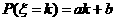 (
(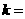 1,2,3,4)。又
1,2,3,4)。又 的数学期望
的数学期望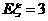 ,则
,则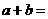 ;
;
解:设离散性随机变量 可能取的值为
可能取的值为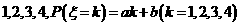 ,所以
,所以
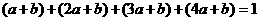 ,即
,即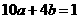 ,又
,又 的数学期望
的数学期望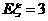 ,则
,则 ,即
,即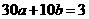 ,
, ,∴
,∴ 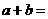
 .
.

