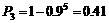38.(山东卷)袋中装着标有数学1,2,3,4,5的小球各2个,从袋中任取3个小球,按3个小球上最大数字的9倍计分,每个小球被取出的可能性都相等,用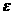 表示取出的3个小球上的最大数字,求:
(1)取出的3个小球上的数字互不相同的概率;
表示取出的3个小球上的最大数字,求:
(1)取出的3个小球上的数字互不相同的概率;
(2)随机变量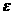 的概率分布和数学期望;
的概率分布和数学期望;
(3)计分介于20分到40分之间的概率.
解:(I)解法一:“一次取出的3个小球上的数字互不相同”的事件记为 ,
,
则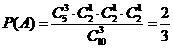
解法二:“一次取出的3个小球上的数字互不相同的事件记为A”,“一次取出的3个小球上有两个数字相同”的事件记为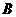 ,则事件
,则事件 和事件
和事件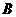 是互斥事件,因为
是互斥事件,因为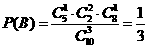 ,所以
,所以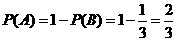 .
.
(II)由题意 有可能的取值为:2,3,4,5.
有可能的取值为:2,3,4,5.
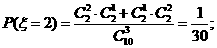
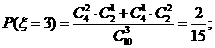
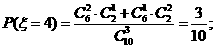
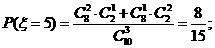
所以随机变量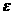 的概率分布为
的概率分布为
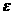 |
2 |
3 |
4 |
5 |
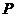 |
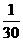 |
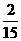 |
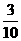 |
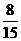 |
因此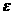 的数学期望为
的数学期望为
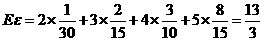
(Ⅲ)“一次取球所得计分介于20分到40分之间”的事件记为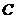 ,则
,则
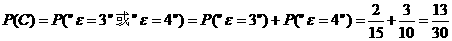
37.(全国II)某批产品成箱包装,每箱5件,一用户在购进该批产品前先取出3箱,再从每箱中任意出取2件产品进行检验。设取出的第一、二、三箱中分别有0件、1件、2件二等品,其余为一等品。
(I)求取6件产品中有1件产品是二等品的概率。
(II)若抽检的6件产品中有2件或2件以上二等品,用户就拒绝购买这批产品,求这批产品被用户拒绝的概率。
解:设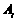 表示事件“第二箱中取出i件二等品”,i=0,1;
表示事件“第二箱中取出i件二等品”,i=0,1;
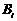 表示事件“第三箱中取出i件二等品”,i=0,1,2;
表示事件“第三箱中取出i件二等品”,i=0,1,2;
(1)依题意所求的概率为
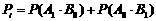
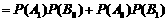
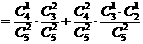
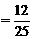
(2)解法一:所求的概率为
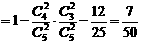
解法二:所求的概率为
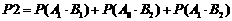
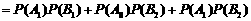
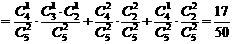
36.(全国II)某批产品成箱包装,每箱5件.一用户在购进该批产品前先取出3箱,再从每箱中任意抽取2件产品进行检验.设取出的第一、二、三箱中分别有0件、1件、2件二等品,其余为一等品.
(Ⅰ)用ξ表示抽检的6件产品中二等品的件数,求ξ的分布列及ξ的数学期望;
(Ⅱ)若抽检的6件产品中有2件或2件以上二等品,用户就拒绝购买这批产品,求这批产品级用户拒绝的概率.
解(1.) 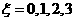
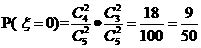
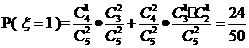
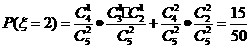
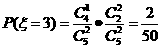
所以 的分布列为
的分布列为
 |
0 |
1 |
2 |
3 |
|
P |
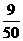 |
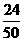 |
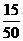 |
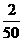 |
 的数学期望E(
的数学期望E( )=
)=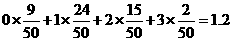
(2)P(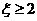 )=
)=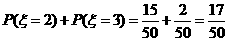
本题主要考察分布列的求法以及利用分布列求期望和概率,难度对于民族地区学生较大
35.(全国卷I)A、B是治疗同一种疾病的两种药,用若干试验组进行对比试验。每个试验组由4只小白鼠组成,其中2只服用A,另2只服用B,然后观察疗效。若在一个试验组中,服用A有效的小白鼠的只数比服用B有效的多,就称该试验组为甲类组。设每只小白鼠服用A有效的概率为 ,服用B有效的概率为
,服用B有效的概率为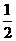 。
。
(Ⅰ)求一个试验组为甲类组的概率;
(Ⅱ)观察3个试验组,求这3个试验组中至少有一个甲类组的概率。
解: (1)设Ai表示事件“一个试验组中,服用A有效的小鼠有i只" , i=0,1,2,
Bi表示事件“一个试验组中,服用B有效的小鼠有i只" , i=0,1,2,
依题意有: P(A1)=2×× = , P(A2)= × = . P(B0)= × = ,
P(B1)=2× × = , 所求概率为: P=P(B0·A1)+P(B0·A2)+P(B1·A2)
= × + × + × =
(Ⅱ)所求概率为: P=1-(1-)3=
34.(全国卷I)A、B是治疗同一种疾病的两种药,用若干试验组进行对比试验。每个试验组由4只小白鼠组成,其中2只服用A,另2只服用B,然后观察疗效。若在一个试验组中,服用A有效的小白鼠的只数比服用B有效的多,就称该试验组为甲类组。设每只小白鼠服用A有效的概率为 ,服用B有效的概率为
,服用B有效的概率为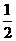 。
。
(Ⅰ)求一个试验组为甲类组的概率;
(Ⅱ)观察3个试验组,用 表示这3个试验组中甲类组的个数,求
表示这3个试验组中甲类组的个数,求 的分布列和数学期望。
的分布列和数学期望。
解: (1)设Ai表示事件“一个试验组中,服用A有效的小鼠有i只" , i=0,1,2,
Bi表示事件“一个试验组中,服用B有效的小鼠有i只" , i=0,1,2,
依题意有: P(A1)=2×× = , P(A2)= × = . P(B0)= × = ,
P(B1)=2× × = , 所求概率为: P=P(B0·A1)+P(B0·A2)+P(B1·A2)
= × + × + × =
(Ⅱ)ξ的可能值为0,1,2,3且ξ~B(3,) . P(ξ=0)=()3= , P(ξ=1)=C31××()2=,
P(ξ=2)=C32×()2× = , P(ξ=3)=( )3=
|
ξ |
0 |
1 |
2 |
3 |
|
P |
|
|
|
|
ξ的分布列为:
33.(辽宁卷)甲、乙两班各派2名同学参加年级数学竞赛,参赛同学成绩及格的概率都为0.6,且参赛同学的成绩相互之间没有影响,求:
(1)甲、乙两班参赛同学中各有1名同学成绩及格的概率;
(2)甲、乙两班参赛同学中至少有1名同学成绩及格的概率.
本小题主要考查相互独立事件的概率乘法公式和互斥事件的概率加法等基础知识,考查学生运用概率知识解决实际问题的能力.
解:(Ⅰ)甲班参赛同学恰有1名同学成绩及格的概率为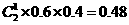
乙班参赛同学中恰有一名同学成绩及格的概率为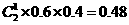
故甲、乙两班参赛同学中各有1名同学成绩几个的概率为
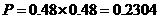
(Ⅱ)解法一:甲、乙两班4名参赛同学成绩都不及格的概率为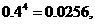
故甲、乙两班参赛同学中至少有一名同学成绩都不及格的概率为
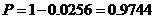
解法二:甲、乙两班参赛同学成绩及格的概率为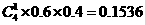
甲、乙两班参赛同学中恰有2名同学成绩及格的概率为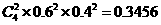
甲、乙两班参赛同学中恰有3名同学成绩及格的概率为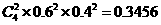
甲、乙两班4同学参赛同学成绩都及格的概率为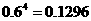
故甲、乙两班参赛同学中至少有1名同学成绩及格的概率为
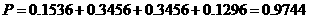
32.(辽宁卷)现有甲、乙两个项目,对甲项目每投资十万元,一年后利润是1.2万元、1.18万元、1.17万元的概率分别为 、
、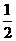 、
、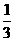 ;已知乙项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是
;已知乙项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是 ,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为
,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为 ,对乙项目每投资十万元,
,对乙项目每投资十万元,  取0、1、2时,
一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量
取0、1、2时,
一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量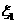 、
、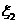 分别表示对甲、乙两项目各投资十万元一年后的利润.
分别表示对甲、乙两项目各投资十万元一年后的利润.
(I) 求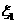 、
、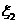 的概率分布和数学期望
的概率分布和数学期望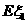 、
、 ;
;
(II) 当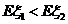 时,求
时,求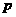 的取值范围.
的取值范围.
[解析](I)解法1:
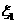 的概率分布为
的概率分布为
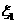 |
1.2 |
1.18 |
1.17 |
|
P |
 |
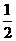 |
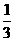 |
E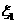 =1.2
=1.2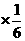 +1.18
+1.18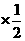 +1.17
+1.17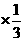 =1.18.
=1.18.
由题设得 ,则
,则 的概率分布为
的概率分布为
 |
0 |
1 |
2 |
|
P |
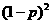 |
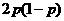 |
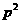 |
故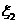 的概率分布为
的概率分布为
 |
1.3 |
1.25 |
0.2 |
|
P |
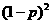 |
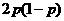 |
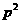 |
所以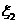 的数学期望为
的数学期望为
E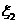 =
=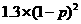 +
+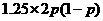 +
+ =
= .
.
解法2: 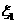 的概率分布为
的概率分布为
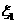 |
1.2 |
1.18 |
1.17 |
|
P |
 |
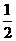 |
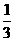 |
E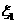 =1.2
=1.2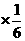 +1.18
+1.18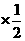 +1.17
+1.17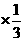 =1.18.
=1.18.
设 表示事件”第i次调整,价格下降”(i=1,2),则
表示事件”第i次调整,价格下降”(i=1,2),则
P( =0)=
=0)= 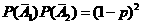 ;
;
P( =1)=
=1)= ;
;
P( =2)=
=2)=
故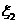 的概率分布为
的概率分布为
 |
1.3 |
1.25 |
0.2 |
|
P |
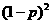 |
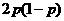 |
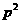 |
所以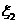 的数学期望为
的数学期望为
E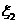 =
=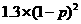 +
+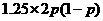 +
+ =
= .
.
(II) 由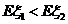 ,得:
,得:

因0<p<1,所以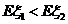 时,p的取值范围是0<p<0.3.
时,p的取值范围是0<p<0.3.
[点评]本小题考查二项分布、分布列、数学期望、方差等基础知识,考查同学们运用概率知识解决实际问题的能力.
31.(江西卷)某商场举行抽奖促销活动,抽奖规则是:从装有9个白球、1个红球的箱子中每次随机地摸出一个球,记下颜色后放回,摸出一个红球获得二得奖;摸出两个红球获得一等奖.现有甲、乙两位顾客,规定:甲摸一次,乙摸两次.求
(1)甲、乙两人都没有中奖的概率;
(2)甲、两人中至少有一人获二等奖的概率.
解:(1)
(2)方法一: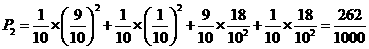
方法二: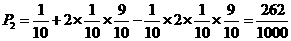
方法三:
30.(江西卷)某商场举行抽奖促销活动,抽奖规则是:从装有9个白球,1个红球的箱子中每次随机地摸出一个球,记下颜色后放回,摸出一个红球可获得奖金10元;摸出2个红球可获得奖金50元,现有甲,乙两位顾客,规定:甲摸一次,乙摸两次,令x表示甲,乙摸球后获得的奖金总额。求:
(1)x的分布列
(2)x的的数学期望
解:(1) 的所有可能的取值为0,10,20,50,60.
的所有可能的取值为0,10,20,50,60.
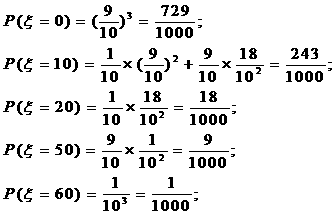
分布列为
|
x |
0 |
10 |
20 |
50 |
60 |
|
P |
  |
 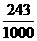 |
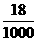 |
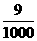 |
 |
 (元)
(元)
29.(湖南卷)某安全生产监督部门对5家小型煤矿进行安全检查(简称安检).若安检不合格,则必须进行整改.若整改后经复查仍不合格,则强行关闭.设每家煤矿安检是否合格是相互独立的,且每家煤矿整改前安检合格的概率是0.5, 整改后安检合格的概率是0.8,计算(结果精确到0.01):
(Ⅰ)恰好有两家煤矿必须整改的概率;
(Ⅱ)平均有多少家煤矿必须整改;
(Ⅲ)至少关闭一家煤矿的概率.
解:(Ⅰ).每家煤矿必须整改的概率是1-0.5,且每家煤矿是否整改是相互独立的.
所以恰好有两家煤矿必须整改的概率是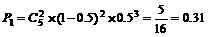 .
.
(Ⅱ).由题设,必须整改的煤矿数 服从二项分布B(5,0.5).从而
服从二项分布B(5,0.5).从而 的数学期望是 E
的数学期望是 E =
= ,即平均有2.50家煤矿必须整改.
,即平均有2.50家煤矿必须整改.
(Ⅲ).某煤矿被关闭,即该煤矿第一次安检不合格,整改后经复查仍不合格,所以该煤矿被关闭的概率是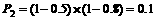 ,从而该煤矿不被关闭的概率是0.9.由题意,每家煤矿是否被关闭是相互独立的,所以至少关闭一家煤矿的概率是
,从而该煤矿不被关闭的概率是0.9.由题意,每家煤矿是否被关闭是相互独立的,所以至少关闭一家煤矿的概率是