(1)设全集U=R,集合M={x| x>1},P={x| x2>1},则下列关系中正确的是 ( )
(A)M=P (B)P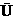 M (C)M
M (C)M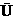 P (D)
P (D)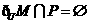
(2)复数 等于 ( )
等于 ( )
(A)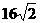 (B)
(B)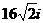 (C)
(C)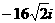 (D)
(D)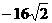
(3)若“p或q”成立的充分条件是“┐r”,则推理:①p或q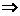 ┐r;②┐r
┐r;②┐r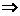 p;③r
p;③r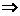 ┐(p或q)
;④┐p且┐q
┐(p或q)
;④┐p且┐q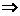 r ,正确的个数为
( )
r ,正确的个数为
( )
(A)0 (B)1 (C) 2 (D)3
(4)已知 是定义在实数集R上的函数,它的反函数为
是定义在实数集R上的函数,它的反函数为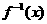 ,若
,若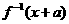 与
与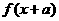 互为反函数,且
互为反函数,且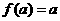 (
(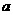 为非零常数),则
为非零常数),则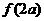 的值为 ( )
的值为 ( )
(A)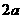 (B)
(B)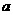 (C)0
(D)
(C)0
(D)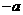
(5)市区某公共汽车站有10个候车位(成一排),现有4名乘客随便坐在某个座位上候车,则恰好有5个连续空座位的候车方式的概率为( )
(A)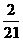 (B)
(B)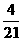 (C)
(C)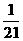 (D)
(D)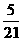
(6)函数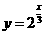 的图象与直线
的图象与直线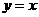 的位置关系是 ( )
的位置关系是 ( )
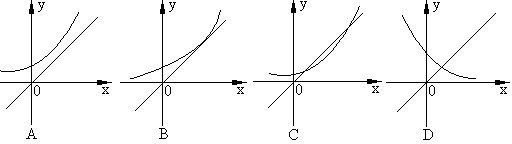 (7)已知
(7)已知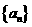 是等比数列,公比为
是等比数列,公比为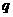 ,设
,设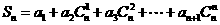 (其中
(其中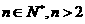 ),且
),且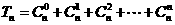 (其中
(其中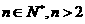 ),如果数列
),如果数列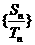 有极限,则公比
有极限,则公比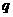 的取值范围是
( )
的取值范围是
( )
(A)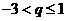 且
且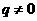 (B)
(B)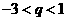 且
且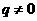
(C)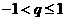 且
且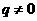 (D)
(D)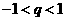 且
且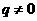
(8)一同学在电脑中按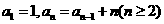 编制一个程序生成若干个实心圆(
编制一个程序生成若干个实心圆(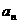 表示第
表示第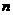 次生成的实心圆的个数)并在每次生成后插入一个空心圆,当某次生成的实心圆个数达到2016时终止,则此时空心圆个数为
( )
次生成的实心圆的个数)并在每次生成后插入一个空心圆,当某次生成的实心圆个数达到2016时终止,则此时空心圆个数为
( )
(A)445 (B)64 (C)63 (D)62
(9)当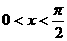 时,函数
时,函数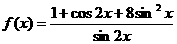 的最小值为
( )
的最小值为
( )
(A)2 (B)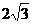 (C)4 (D)
(C)4 (D)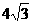
(10)已知向量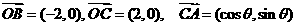 ,则
,则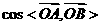 的取值范围是
( )
的取值范围是
( )
(A)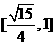 (B)
(B)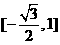 (C)
(C)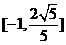 (D)
(D)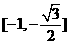
20.(本小题满分14分)
(理)若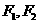 为双曲线
为双曲线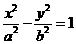 的左,右焦点,
的左,右焦点, 为坐标原点,
为坐标原点,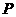 在双曲线左支上,
在双曲线左支上,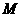 在右准线上,且满足
在右准线上,且满足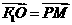 ,
,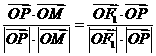 .
.
(1)求此双曲线的离心率;(2)若此双曲线过点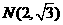 ,求双曲线方程;(3)设(2)中双曲线的虚轴端点为
,求双曲线方程;(3)设(2)中双曲线的虚轴端点为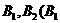 在
在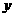 轴正半轴上),点
轴正半轴上),点 在双曲线上,且
在双曲线上,且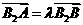 ,求
,求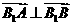 时,直线
时,直线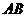 的方程.
的方程.
(文)已知
(1) 求点P(x,y)的轨迹C的方程;
(2) 若直线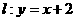 与曲线C交于P、Q两点,求|PQ|的长;
与曲线C交于P、Q两点,求|PQ|的长;
(3) 若直线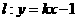 与曲线C交于A、B两点,并且A、B在y轴的同一侧,求实数k的取值范围。
与曲线C交于A、B两点,并且A、B在y轴的同一侧,求实数k的取值范围。
19.(本小题满分14分)
设数列{an}的前n项和为Sn ,且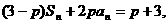 其中p为常数,且
其中p为常数,且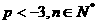 (说明:①、②、③、④理科考生答,①、②文科考生答.)
(说明:①、②、③、④理科考生答,①、②文科考生答.)
①求证:数列{an}是等比数列,并求出数列{an}的通项公式 ;
②若数列{an}的公比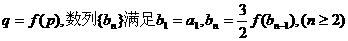 求出数列
求出数列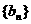 的通项公式;
的通项公式;
③在②的条件下, 求实数
求实数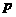 的值;
的值;
④在③的条件下,又数列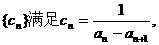 求无穷数列
求无穷数列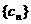 的各项和.
的各项和.
18.
 (本小题满分14分)银行按规定在一定时间结算利息一次,结息后即将利息并入本金,这种计算方法叫做复利,现在某企业进行技术改造,有两种方案;甲方案:一次性贷款10万元,第一年可获利1万元,以后每年比前一年增加30%的利润;乙方案:每年贷款1万元,第一年可获利1万元,以后每年比前一年增加5千元。两种方案的贷款使用期都是10年,到期一次性还本付息,若银行贷款利率是按年息10%的复利计算,试比较两种方案的优劣(计算时精确到千元,并取1.110
(本小题满分14分)银行按规定在一定时间结算利息一次,结息后即将利息并入本金,这种计算方法叫做复利,现在某企业进行技术改造,有两种方案;甲方案:一次性贷款10万元,第一年可获利1万元,以后每年比前一年增加30%的利润;乙方案:每年贷款1万元,第一年可获利1万元,以后每年比前一年增加5千元。两种方案的贷款使用期都是10年,到期一次性还本付息,若银行贷款利率是按年息10%的复利计算,试比较两种方案的优劣(计算时精确到千元,并取1.110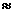 2.594,1.310
2.594,1.310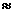 13.79).
13.79).
17.(本小题满分14分)已知:如图,矩形ABCD,PA⊥平面ABCD, M、N、R分别是AB、PC、CD的中点,
①求证:直线AR∥平面PMC ;
②求证:直线MN⊥直线AB ;
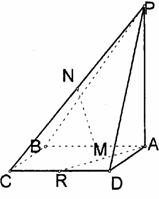 ③若平面PDC与平面ABCD所成的二面角为
③若平面PDC与平面ABCD所成的二面角为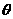 ,能否确定
,能否确定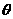 使直线MN是异面直线AB与PC的公垂线,若能确定,求出
使直线MN是异面直线AB与PC的公垂线,若能确定,求出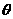 的值,若不能确定,说明理由.
的值,若不能确定,说明理由.
16.(本题满分14分)已知函数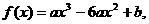 问是否存在实数a、b使f(x)在
问是否存在实数a、b使f(x)在
[-1,2]上取得最大值3,最小值-29,若存在,求出a、b的值.并指出函数的单调区间 . 若不存在,请说明理由 .
14.已知函数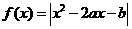 (
(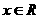 ),下列命题中正确命题的序号为
),下列命题中正确命题的序号为
(1)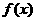 必为偶函数;
必为偶函数;
(2)当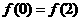 时,
时,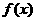 的图象关于直线
的图象关于直线 对称;
对称;
(3)若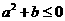 ,则
,则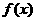 在区间
在区间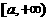 上是增函数;
上是增函数;
(4)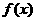 的最大值为
的最大值为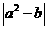 .
.
12.(理)若(2x2-1)n的展开式中各项系数和为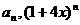 的展开式中各项系数和为
的展开式中各项系数和为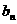 ,则
,则
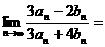 .
.
(文)已知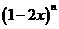 的展开式中,二项式系数的和为64,则它的二项展开式的中间项是_________________
的展开式中,二项式系数的和为64,则它的二项展开式的中间项是_________________

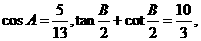 求:
求: 的值;
(2)
的值;
(2)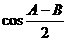 的值.
的值.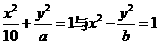 有相同的焦点,它们的一个公共点为
有相同的焦点,它们的一个公共点为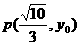 ,则
,则