9.★用数学归纳法证明命题“n3+(n+1)3+(n+2)3(n∈N)能被9整除”,要利用归纳假设证n=k+1时的情况,只需展开( )
A.(k+3)3 B.(k+2)3
C.(k+1)3 D.(k+1)3+(k+2)3
分析 本题考查用数学归纳法证明整除性问题.只需把n=k+1时的情况拼凑成一部分为假设的形式,另一部分为除数的倍数形式即可.
解 当n=k+1时,被除数为(k+1)3+(k+2)3+(k+3)3=k3+(k+1)3+(k+2)3+9(k2+3k+3).故只需展开(k+3)3即可.
答案 A
8.★欲用数学归纳法证明对于足够大的自然数n,总有2n>n3,n0为验证的第一个值,则( )
A.n0=1
B.n0为大于1小于10的某个整数
C.n0≥10
D.n0=2
解析 本题考查用数学归纳法证明问题时,第一步初始值n0的确定.不能认为初始值都从n0=1开始,需根据实际题目而定.当1≤n<10时,2n与n3的大小不确定,而当n≥10时,总有2n>n3.
答案 C
7.★已知数列{an}是由正数组成的数列,a1=3,且满足lgan=lgan-1+lgc,其中n>1且为整数,c>2,则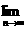
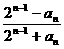 等于( )
等于( )
A.-1
B.1 C.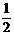 D.
D.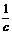
分析 本题考查数列的极限及运算能力.
解 ∵an>0,lgan=lgan-1+lgc,
∴an=an-1·c,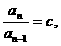 =c,
=c,
即数列{an}是首项为a1=3,公比为c的等比数列,an=3·cn-1(c>2),
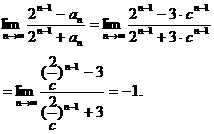
答案 A
6.
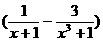 等于( )
等于( )
A.0 B.-1 C.1 D.不存在
分析 本题考查函数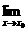 f(x)的极限.若把x=-1代入函数解析式,解析式无意义,故应化简函数解析式,约去使它的分母为0的因式,再求解.
f(x)的极限.若把x=-1代入函数解析式,解析式无意义,故应化简函数解析式,约去使它的分母为0的因式,再求解.
解 
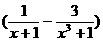 =
=
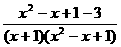
=
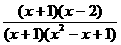 =
=
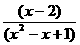
=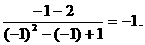
答案 B
5.★若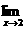
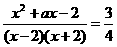 ,则a的值为( )
,则a的值为( )
A.0
B.1
C.-1
D.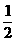
分析 本题考查当x→x0时函数的极限.
解 ∵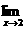
 存在,而把x=2代入分母时,分母为零,
存在,而把x=2代入分母时,分母为零,
∴分子、分母应有(x-2)这一公因式,化简以后,再求极限.
∴分子x2+ax-2可分解成(x-2)(x+1),
即x2+ax-2=(x-2)(x+1)=x2-x-2.
∴a=-1.
答案 C
4.数列1,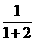 ,
,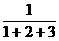 ,
,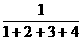 ,…,
,…,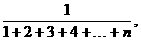 …的前n项和为Sn,则
…的前n项和为Sn,则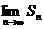 等于( )
等于( )
A.0
B.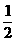 C.1
D.2
C.1
D.2
分析 本题考查数列极限的求法.要求数列{an}的前n项和,应首先确定它的通项公式.
解 ∵an=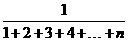 =
=
∴Sn=a1+a2+…+an=2(1-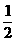 +
+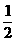 -
-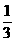 +…+
+…+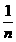 -
-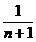 )=
)=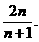 .
.
∴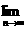 Sn=
Sn=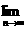
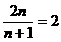 .
.
答案 D
3.用数学归纳法证明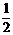 +cosα+cos3α+…+cos(2n-1)α=
+cosα+cos3α+…+cos(2n-1)α=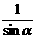 ·
· ·
·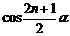
(α≠kπ,n∈N*),验证n=1等式成立时,左边计算所得的项是( )
A.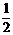 B.
B.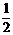 +cosα
+cosα
C.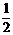 +cosα+cos3α
D.
+cosα+cos3α
D.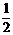 +cosα+cos3α+cos5α
+cosα+cos3α+cos5α
分析 分清等式左边的构成情况是解决此题的关键;对于本题也可把n=1代入右边化简得出左边.
解法一 因为等式的左边是(n+1)项的形式,故n=1时,应保留两项,它们是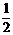 +cosα.
+cosα.
解法二 当n=1时,右边=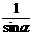 sin
sin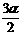 cos
cos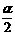 =
=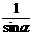 ·
·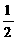 (sin2α+sinα)=
(sin2α+sinα)=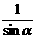 (sinαcosα+
(sinαcosα+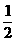 sinα)=
sinα)=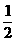 +cosα.
+cosα.
答案 B
2.设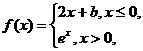 ,若
,若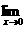 f(x)存在,则常数b的值是( )
f(x)存在,则常数b的值是( )
A.0 B.1 C.-1 D.e
分析 本题考查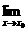 f(x)=a的充要条件:
f(x)=a的充要条件:
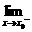 f(x)=
f(x)=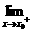 f(x)=a.
f(x)=a.
解 ∵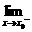 (2x+b)=b,
(2x+b)=b,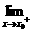 ex=1,
ex=1,
又条件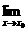 f(x)存在,∴b=1.
f(x)存在,∴b=1.
答案 B
1.式子12+22+32+…+n2=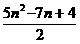 在( )
在( )
A.n为任何自然数时都成立
B.n=1,2时成立,n=3时不成立
C.n=4时成立,n=5时不成立
D.n=3时成立,n=4时不成立
解析用数学归纳法证题的前提是分清等式两边的构成情况,就本题而言,它的左边是从1开始的n个连续正整数的平方和的形式,可采用直接代入法求解.
答案 D
22.(本小题满分14分)已知函数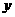 =
=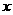 +
+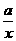 有如下性质:如果常数
有如下性质:如果常数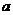 >0,那么该函数在
>0,那么该函数在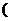 0,
0,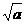
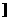 上是减函数,在
上是减函数,在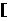
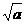 ,+∞
,+∞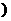 上是增函数.
上是增函数.
(1)如果函数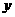 =
=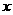 +
+ (
(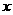 >0)的值域为
>0)的值域为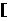 6,+∞
6,+∞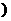 ,求
,求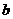 的值;
的值;
(2)研究函数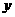 =
=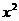 +
+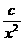 (常数
(常数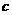 >0)在定义域内的单调性,并说明理由;
>0)在定义域内的单调性,并说明理由;
(3)对函数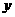 =
=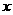 +
+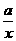 和
和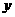 =
=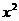 +
+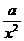 (常数
(常数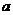 >0)作出推广,使它们都是你所推广的函数的特例.
>0)作出推广,使它们都是你所推广的函数的特例.
(4)(理科生做)研究推广后的函数的单调性(只须写出结论,不必证明),并求函数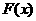 =
=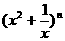 +
+ (
(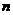 是正整数)在区间[
是正整数)在区间[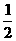 ,2]上的最大值和最小值(可利用你的研究结论).
,2]上的最大值和最小值(可利用你的研究结论).
南昌市高中新课程方案试验高三复习训练题

