《2025年点石成金金牌夺冠九年级数学全一册人教版辽宁专版》

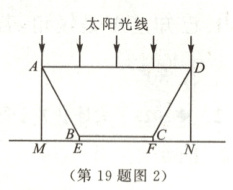
19. (11分)◆2024·江西中考◆如图1是世界第一“大碗”——景德镇昌南里文化艺术中心主体建筑,其造型灵感来自于宋代湖田窑影青斗笠碗,寓意“万瓷之母”.如图2是“大碗”的切面示意图,“大碗”由主体$ABCD$和矩形碗底$BEFC$组成.已知$AD // EF$,$AM$,$DN$是太阳光线,$AM \perp MN$于点$M$,$DN \perp MN$于点$N$,点$M$,$E$,$F$,$N$在同一条直线上.经测量$ME = FN = 20 m$,$EF = 40 m$,$BE = 2.4 m$,$\angle ABE = 152°$.(结果取整数.参考数据:$\sin 62° \approx 0.88$,$\cos 62° \approx 0.47$,$\tan 62° \approx 1.88$)
(1)求“大碗”的口径$AD$的长.
(2)求“大碗”的高度$AM$的长.

答案：
19.解:
(1)
∵AD//EF，点M，E，F，N在同一条直线上，
∴AD//MN.
∵AM⊥MN，DN⊥MN，
∴∠AMN=90°，∠DNM=90°.
∴∠AMN+∠DNM=180°.
∴AM//DN.
∴四边形AMND是平行四边形.
∴AD=MN=ME+EF+FN=80(m).
答:“大碗”的口径AD是80m.
(2)如图，过点B作BG⊥AM于点G.
∴∠BGM=∠BGA=90°.
∵四边形BEFC是矩形，
∴∠BEF=90°.
∴∠BEM=90°.
∵∠GME=90°，
∴四边形GMEB是矩形.
∴GM=BE=2.4，GB=ME=20，∠GBE=90°.
∵∠ABE=152°，
∴∠ABG=∠ABE−∠GBE=62°.在Rt△AGB中，
∵tan∠ABG=$\frac{AG}{GB}$，
∴AG=GB·tan62°≈20×1.88=37.6.
∴AM=AG+GM≈40(m).
答:“大碗”的高度AM约是40m.

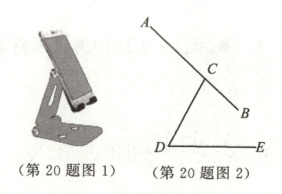
20. (12分)如图1是一种手机支架,图2是其侧面结构示意图.托板$AB$固定在支撑板顶端的点$C$处,托板$AB$可绕点$C$转动,支撑板$CD$可绕点$D$转动.现量得$CD = 10 cm$,$AC = 12 cm$.
(1)当支撑板$CD$与底座$DE$的夹角$\angle CDE = 60°$时,求点$C$到底座$DE$的距离.(结果保留根号)
(2)小强在使用过程中发现,当$\angle CDE = 60°$,$\angle ACD = 105°$时,此支架使用起来最舒适,求此时点$A$到底座$DE$的距离.(结果保留根号)

答案：
20.解:
(1)如图1，过点C作CF⊥DE于点F.
∴∠CFD=90°.
∴∠DCF=90°−∠CDF=30°.
∴DF=$\frac{1}{2}$CD=5cm.　
由勾股定理，得CF=$\sqrt{CD^{2}-DF^{2}}$=5$\sqrt{3}$(cm).
答:点C到底座DE的距离是5$\sqrt{3}$cm.

(2)如图2，过点C作CF⊥DE于点F，过点A作AG⊥DE，交ED的延长线于点G，过点C作CH⊥AG于点H.
∴∠CFG=90°，∠G=90°，∠CHG=∠CHA=90°.
∴四边形HGFC是矩形.
∴HG=CF，∠HCF=90°.
∵∠CDE=60°，
∴∠DCF=30°.
由
(1)可知CF=5$\sqrt{3}$.
∴HG=5$\sqrt{3}$.
∵∠ACD=105°，
∴∠ACH=∠ACD+∠DCF−∠HCF=45°.
在Rt△AHC中，
∵sin∠ACH=$\frac{AH}{AC}$，
∴AH=AC·sin45°=6$\sqrt{2}$.
∴AG=AH+HG=(6$\sqrt{2}$+5$\sqrt{3}$)cm.
答:此时点A到底座DE的距离是(6$\sqrt{2}$+5$\sqrt{3}$)cm.