《2025年点石成金金牌夺冠九年级数学全一册人教版辽宁专版》

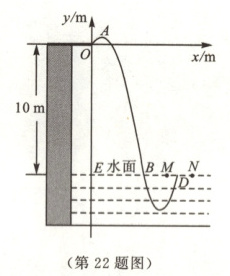
22. (12 分)2024 年 4 月 21 日晚，为期 3 天的 2024 年世界泳联跳水世界杯总决赛在西安奥体中心游泳跳水馆落下帷幕，中国跳水“梦之队”在本次赛事参加的 8 个项目中全部获得了金牌.某数学兴趣小组对跳水训练进行实践调查，某跳水运动员在 10 m 跳台上进行跳水训练，建立如图所示的平面直角坐标系，水面与$y$轴交于点$E(0,-10)$.运动员(看成一点)在空中运动的路线是经过原点$O$的抛物线，在跳某个规定动作时，运动员在空中最高处点$A$的坐标是$(\frac{3}{4},\frac{9}{16})$，且运动员在距离水面 5 m 之前，必须完成规定动作，并调整好入水姿势，否则就会出现失误.运动员入水后的运动路线是另一条抛物线.
(1)求运动员在空中运动时对应的抛物线的解析式及入水处点$B$的坐标.
(2)若运动员在空中调整好入水姿势时，与$y$轴的水平距离是 3 m，该运动员此次跳水会不会出现失误? 请说明理由.
(3)在该运动员入水处点$B$的正前方有$M$，$N$两点，且$EM=6 m$，$EN=8 m$，该运动员入水后的运动路线对应的抛物线解析式为$y=(x-h)^{2}+k$.若该运动员出水处点$D$在点$M$，$N$之间(包括点$M$，$N$)，求$k$的取值范围.

答案： 22.解:
(1)设运动员在空中运动时对应的抛物线的解析式为y=a(x−$\frac{3}{4}$)²+$\frac{9}{16}$。
∵抛物线经过原点，
∴将(0,0)代入y=a(x−$\frac{3}{4}$)²+$\frac{9}{16}$，得$\frac{9}{16}$a+$\frac{9}{16}$=0。
解得a=−1。
∴运动员在空中运动时对应的抛物线的解析式为y=−(x−$\frac{3}{4}$)²+$\frac{9}{16}$=−x²+$\frac{3}{2}$x。
当y=−10时,−x²+$\frac{3}{2}$x=−10。
解得x1=4,x2=−$\frac{5}{2}$(不合题意，舍去)。
∴点B的坐标是(4,−10)。
(2)不会出现失误。
理由:
∵运动员在空中调整好入水姿势时,与y轴的水平距离是3m,
∴运动员调整好入水姿势时对应点的横坐标是3。
当x=3时,y=−3²+$\frac{3}{2}$×3=−$\frac{9}{2}$。
∴运动员调整好入水姿势时对应点的坐标是(3,−$\frac{9}{2}$)。
∴运动员此时与水面的距离是−$\frac{9}{2}$−(−10)=$\frac{11}{2}$。
∵$\frac{11}{2}$＞5,
∴运动员此次跳水不会出现失误。
(3)
∵点B(4,−10)在y=(x−h)²+k上,
∴代入,得−10=(4−h)²+k。
∴k=−(h−4)²−10,即k是关于h 的二次函数,且该抛物线的对称轴是直线h=4,开口向下。
∵EM=6,EN=8,点E(0,−10),
∴点M(6,−10),N(8,−10)。
∵出水处点D在点M,N之间(包括点M,N),
∴将点B(4,−10),M(6,−10)代入y=(x−h)²+k,
得$\begin{cases}(4 - h)^{2} + k = -10\\(6 - h)^{2} + k = -10\end{cases}$，解得$\begin{cases}h = 5\\k = -11\end{cases}$。
将点B(4,−10),N(8,−10)代入y=(x−h)²+k,
得$\begin{cases}(4 - h)^{2} + k = -10\\(8 - h)^{2} + k = -10\end{cases}$，解得$\begin{cases}h = 6\\k = -14\end{cases}$。
∴5≤h≤6。
∵当5≤h≤6时,k随h的增大而减小，
∴k的取值范围是−14≤k≤−11。