2025年点石成金金牌夺冠九年级数学全一册人教版辽宁专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年点石成金金牌夺冠九年级数学全一册人教版辽宁专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
14. ◆$2024·$重庆中考◆ 如图,在$\triangle ABC$中,延长$AC$至点$D$,使$CD=CA$,过点$D$作$DE//CB$,且$DE=DC$,连接$AE$交$BC$于点$F$.若$\angle CAB=\angle CFA$,$CF=1$,则$BF$的长是

3
.
答案:
14.3 [解析]
∵DE//CB,
∴△ACF∽△ADE.
∴$\frac{CF}{DE}$=$\frac{AC}{AD}$.
∵CF=1,AC=CD=DE,
∴AD=2AC.
∴$\frac{1}{AC}$=$\frac{AC}{2AC}$.
∴AC=2.
∵∠CAB=∠CFA,∠ACB=∠FCA,
∴△CAB∽△CFA.
∴$\frac{CA}{CF}$=$\frac{BC}{AC}$.
∴$\frac{2}{1}$=$\frac{BF + 1}{2}$.
∴BF=3.
∵DE//CB,
∴△ACF∽△ADE.
∴$\frac{CF}{DE}$=$\frac{AC}{AD}$.
∵CF=1,AC=CD=DE,
∴AD=2AC.
∴$\frac{1}{AC}$=$\frac{AC}{2AC}$.
∴AC=2.
∵∠CAB=∠CFA,∠ACB=∠FCA,
∴△CAB∽△CFA.
∴$\frac{CA}{CF}$=$\frac{BC}{AC}$.
∴$\frac{2}{1}$=$\frac{BF + 1}{2}$.
∴BF=3.
15. 如图,正方形$ABCD$的边长是4,点$E$,$F$分别是$BC$,$CD$的中点,连接$AE$,$DE$,$BF$.若$AE$,$DE$分别交$BF$于点$G$,$H$,则$GH$的长是
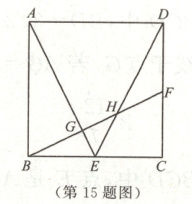
$\frac{8\sqrt{5}}{15}$
.
答案:
15.$\frac{8\sqrt{5}}{15}$ [解析]如图,取DE的中点M,连接MF.
∵点F是DC的中点,
∴MF是△DEC的中位线.
∴MF=$\frac{1}{2}$EC,MF//BC.
∵点E,F分别是BC,CD的中点,正方形ABCD的边长是4,
∴AB=BC=CD=4,BE=CF=2,∠ABE=∠BCF=90°.
∴△ABE≌△BCF(SAS).
∴∠BAE=∠CBF.
∵∠BAE+∠BEA=90°,
∴∠CBF+∠BEA=90°.
∴∠BGE=90°.
∴∠BGE=∠BCF.
∵∠GBE=∠CBF,
∴△BGE∽△BCF.
∴$\frac{BE}{BF}$=$\frac{BG}{BC}$.由勾股定理,得BF=2$\sqrt{5}$.
∴$\frac{2}{2\sqrt{5}}$=$\frac{BG}{4}$.解得BG=$\frac{4\sqrt{5}}{5}$.
∵MF//BC,
∴易证△BEH∽△FMH.
∴$\frac{BE}{FM}$=$\frac{BH}{FH}$.
∵FM=$\frac{1}{2}$EC=1,
∴$\frac{2}{1}$=$\frac{BH}{FH}$.
∴BH=2FH.
∴FH=$\frac{1}{3}$BF=$\frac{2\sqrt{5}}{3}$.
∴GH=BF−BG−FH=$\frac{8\sqrt{5}}{15}$.
15.$\frac{8\sqrt{5}}{15}$ [解析]如图,取DE的中点M,连接MF.
∵点F是DC的中点,
∴MF是△DEC的中位线.
∴MF=$\frac{1}{2}$EC,MF//BC.
∵点E,F分别是BC,CD的中点,正方形ABCD的边长是4,
∴AB=BC=CD=4,BE=CF=2,∠ABE=∠BCF=90°.
∴△ABE≌△BCF(SAS).
∴∠BAE=∠CBF.
∵∠BAE+∠BEA=90°,
∴∠CBF+∠BEA=90°.
∴∠BGE=90°.
∴∠BGE=∠BCF.
∵∠GBE=∠CBF,
∴△BGE∽△BCF.
∴$\frac{BE}{BF}$=$\frac{BG}{BC}$.由勾股定理,得BF=2$\sqrt{5}$.
∴$\frac{2}{2\sqrt{5}}$=$\frac{BG}{4}$.解得BG=$\frac{4\sqrt{5}}{5}$.
∵MF//BC,
∴易证△BEH∽△FMH.
∴$\frac{BE}{FM}$=$\frac{BH}{FH}$.
∵FM=$\frac{1}{2}$EC=1,
∴$\frac{2}{1}$=$\frac{BH}{FH}$.
∴BH=2FH.
∴FH=$\frac{1}{3}$BF=$\frac{2\sqrt{5}}{3}$.
∴GH=BF−BG−FH=$\frac{8\sqrt{5}}{15}$.

16. (13分)◆$2024·$锦州期末◆ 如图,在$\triangle ABC$中,$AB=AC$,延长$AB$至点$D$,使$BD=BC$,延长$BC$至点$E$,连接$DE$,$AE$,且$\angle D=\angle AEC$.若$BC=3$,$CE=2$,求$AD$的长.
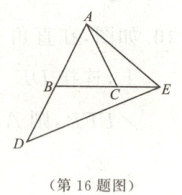

答案:
16.解:
∵AB=AC,
∴∠ABC=∠ACB.
∵∠EBD=180°−∠ABC,∠ACE=180°−∠ACB,
∴∠EBD=∠ACE.
∵∠D=∠AEC,
∴△DBE∽△ECA.
∴$\frac{BD}{CE}$=$\frac{BE}{CA}$.
∵BC=3,CE=2,
∴BD=3,BE=5.
∴$\frac{3}{2}$=$\frac{5}{CA}$.
∴CA=$\frac{10}{3}$.
∴AB=$\frac{10}{3}$.
∴AD=AB+BD=$\frac{19}{3}$.
∵AB=AC,
∴∠ABC=∠ACB.
∵∠EBD=180°−∠ABC,∠ACE=180°−∠ACB,
∴∠EBD=∠ACE.
∵∠D=∠AEC,
∴△DBE∽△ECA.
∴$\frac{BD}{CE}$=$\frac{BE}{CA}$.
∵BC=3,CE=2,
∴BD=3,BE=5.
∴$\frac{3}{2}$=$\frac{5}{CA}$.
∴CA=$\frac{10}{3}$.
∴AB=$\frac{10}{3}$.
∴AD=AB+BD=$\frac{19}{3}$.
17. (13分)如图,在矩形$ABCD$中,点$E$是$DC$上的一点,把$\triangle ADE$沿$AE$翻折,使点$D$恰好落在$BC$边上的点$F$处.
(1)求证:$\triangle ABF \backsim \triangle FCE$.
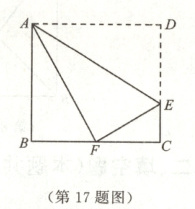
(2)若$AB=2\sqrt{3}$,$AD=4$,求$CE$的长.
(1)求证:$\triangle ABF \backsim \triangle FCE$.

(2)若$AB=2\sqrt{3}$,$AD=4$,求$CE$的长.
答案:
17.
(1)证明:
∵四边形ABCD是矩形,
∴∠B=∠C=∠D=90°.
∴∠AFB+∠BAF=90°.由翻折的性质可知,∠AFE=∠D=90°.
∴∠AFB+∠CFE=90°,
∴∠BAF=∠CFE.
∴△ABF∽△FCE.
(2)解:
∵四边形ABCD是矩形,
∴AD=BC=4.由翻折的性质可知,AF=AD=4.
∵AB=2$\sqrt{3}$,
∴由勾股定理,得$BF=\sqrt{AF^{2}-AB^{2}}=\sqrt{4^{2}-(2\sqrt{3})^{2}}=2$.
∴CF=BC−BF=2.由
(1)得△ABF∽△FCE.
∴$\frac{BF}{CE}$=$\frac{AB}{FC}$.
∴$\frac{2}{CE}$=$\frac{2\sqrt{3}}{2}$.
∴$CE=\frac{2\sqrt{3}}{3}$.
(1)证明:
∵四边形ABCD是矩形,
∴∠B=∠C=∠D=90°.
∴∠AFB+∠BAF=90°.由翻折的性质可知,∠AFE=∠D=90°.
∴∠AFB+∠CFE=90°,
∴∠BAF=∠CFE.
∴△ABF∽△FCE.
(2)解:
∵四边形ABCD是矩形,
∴AD=BC=4.由翻折的性质可知,AF=AD=4.
∵AB=2$\sqrt{3}$,
∴由勾股定理,得$BF=\sqrt{AF^{2}-AB^{2}}=\sqrt{4^{2}-(2\sqrt{3})^{2}}=2$.
∴CF=BC−BF=2.由
(1)得△ABF∽△FCE.
∴$\frac{BF}{CE}$=$\frac{AB}{FC}$.
∴$\frac{2}{CE}$=$\frac{2\sqrt{3}}{2}$.
∴$CE=\frac{2\sqrt{3}}{3}$.
18. (14分)如图,在四边形$ABCD$中,$AD//BC$,$AB>CD$,点$E$,$F$分别在线段$AC$,$BC$上,且$\angle FAC=\angle EDA$,$\angle ACD=\angle ADC$.
(1)求证:$AF=DE$.
(2)若$AF^2=BF· CE$,求证:$\angle ABC=\angle CDE$.

(1)求证:$AF=DE$.
(2)若$AF^2=BF· CE$,求证:$\angle ABC=\angle CDE$.

答案:
18.证明:
(1)
∵∠ACD=∠ADC,
∴AC=DA.
∵AD//BC,
∴∠DAE=∠ACF.
∵∠FAC=∠EDA,
∴△CAF≌△ADE(ASA).
∴AF=DE.
(2)
∵△CAF≌△ADE,
∴∠CFA=∠AED.
∵∠AFB=180°−∠CFA,∠CED=180°−∠AED,
∴∠AFB=∠CED.
∵$AF^{2}=BF· CE$,
∴$\frac{AF}{CE}$=$\frac{BF}{AF}$.
∵AF=DE,
∴$\frac{AF}{CE}$=$\frac{BF}{DE}$.
∴△ABF∽△CDE.
∴∠ABC=∠CDE.
(1)
∵∠ACD=∠ADC,
∴AC=DA.
∵AD//BC,
∴∠DAE=∠ACF.
∵∠FAC=∠EDA,
∴△CAF≌△ADE(ASA).
∴AF=DE.
(2)
∵△CAF≌△ADE,
∴∠CFA=∠AED.
∵∠AFB=180°−∠CFA,∠CED=180°−∠AED,
∴∠AFB=∠CED.
∵$AF^{2}=BF· CE$,
∴$\frac{AF}{CE}$=$\frac{BF}{AF}$.
∵AF=DE,
∴$\frac{AF}{CE}$=$\frac{BF}{DE}$.
∴△ABF∽△CDE.
∴∠ABC=∠CDE.
查看更多完整答案,请扫码查看


