2025年拔尖特训四年级数学上册北师大版广东专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年拔尖特训四年级数学上册北师大版广东专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第21页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
6.(深圳龙华区)斯诺克又称障碍桌球,是桌球比赛的一种。2022年10月6日至9日,香港世界斯诺克大师赛在我国香港红磡体育馆举行。
(1)小华与爸爸一起去观看比赛,他发现,当球撞击桌边后,就会弹向另一个方向。下面三幅图是桌球三次不同的模拟行进路线。请观察桌球射入路线与桌边的夹角、弹出路线与桌边的夹角,然后猜一猜,量一量,你能得出什么结论?
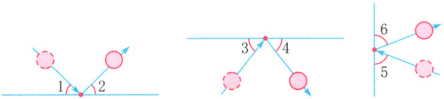
(2)运用(1)中的结论,请你补全下面桌球的两次模拟行进路线。

(1)小华与爸爸一起去观看比赛,他发现,当球撞击桌边后,就会弹向另一个方向。下面三幅图是桌球三次不同的模拟行进路线。请观察桌球射入路线与桌边的夹角、弹出路线与桌边的夹角,然后猜一猜,量一量,你能得出什么结论?

(2)运用(1)中的结论,请你补全下面桌球的两次模拟行进路线。

答案:
6.
(1)$\angle1 = \angle2$,$\angle3 = \angle4$,$\angle5 = \angle6$,桌球射入路线与桌边的夹角和弹出路线与桌边的夹角相等
(2)

6.
(1)$\angle1 = \angle2$,$\angle3 = \angle4$,$\angle5 = \angle6$,桌球射入路线与桌边的夹角和弹出路线与桌边的夹角相等
(2)

7.(思维过程)小飞将一张长方形纸按如图所示的方式折叠,已知$\angle1 = 30^{\circ}$,$\angle2 = 20^{\circ}$,则$\angle3$是多少度?
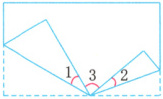
思路提示:通过观察,分析出由折叠得到的哪两个角相等,并抓住平角是$180^{\circ}$来求解。

思路提示:通过观察,分析出由折叠得到的哪两个角相等,并抓住平角是$180^{\circ}$来求解。
答案:
7.$(30^{\circ} + 20^{\circ}) × 2 = 100^{\circ}$ $180^{\circ} - 100^{\circ} = 80^{\circ}$
解析:如图,由折叠的性质可知,$\angle4 = \angle1 = 30^{\circ}$,$\angle5 = \angle2 = 20^{\circ}$,而$\angle1$,$\angle2$,$\angle3$,$\angle4$,$\angle5$正好组成一个平角,由此可求出$\angle3$的度数。

7.$(30^{\circ} + 20^{\circ}) × 2 = 100^{\circ}$ $180^{\circ} - 100^{\circ} = 80^{\circ}$
解析:如图,由折叠的性质可知,$\angle4 = \angle1 = 30^{\circ}$,$\angle5 = \angle2 = 20^{\circ}$,而$\angle1$,$\angle2$,$\angle3$,$\angle4$,$\angle5$正好组成一个平角,由此可求出$\angle3$的度数。

8.下图中一共有()条线段。

思路提示:数线段时,先数出一条线段上的基本线段有$n$条,再根据“线段总条数$= 1 + 2 + 3 + ·s + n$”来计算。

思路提示:数线段时,先数出一条线段上的基本线段有$n$条,再根据“线段总条数$= 1 + 2 + 3 + ·s + n$”来计算。
答案:
36
9.已知$\angle1 = \angle2 = \angle3 = \angle4 = 20^{\circ}$,则图中所有锐角的度数之和是多少?

思路提示:先数出有$n$个基本角,再根据“角的总个数$= 1 + 2 + 3 + ·s + n$”计算角的总个数,最后根据不同角的度数求和。

思路提示:先数出有$n$个基本角,再根据“角的总个数$= 1 + 2 + 3 + ·s + n$”计算角的总个数,最后根据不同角的度数求和。
答案:
9.$20^{\circ} × 4 + 40^{\circ} × 3 + 60^{\circ} × 2 + 80^{\circ} = 400^{\circ}$
解析:有4个基本角,每个基本角都是$20^{\circ}$,由2个基本角组成的$40^{\circ}$的角有3个,由3个基本角组成的$60^{\circ}$的角有2个,由4个基本角组成的$80^{\circ}$的角有1个,最后将所有锐角的度数相加即可。
解析:有4个基本角,每个基本角都是$20^{\circ}$,由2个基本角组成的$40^{\circ}$的角有3个,由3个基本角组成的$60^{\circ}$的角有2个,由4个基本角组成的$80^{\circ}$的角有1个,最后将所有锐角的度数相加即可。
查看更多完整答案,请扫码查看


