第20页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
2. (2024·台州黄岩)按要求在下面的梯形中画一条线段,把梯形分成两个图形。(9 分)


答案:
(1)
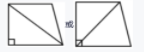
(2)

(3)
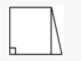
(1)

(2)

(3)

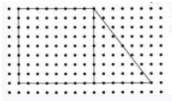
3. (2025·安吉)已知右图中的每个小正方形边长是 $1$ cm。(12 分)
(1)量一量:$\angle ABC = ($ $ )°$,它是一个( )角。(4 分)

(2)画出表示点 $P$ 到线段 $AB$ 和 $BC$ 之间距离的线段。(4 分)
(3)在格子图中找平行四边形的第四个顶点 $D$,连接 $AD$、$CD$,画出平行四边形 $ABCD$。(2 分)
(4)在格子图中找出点 $E$,使四边形 $ABCE$ 是梯形,且上、下底的差为 $2$ cm。这样的点 $E$ 有( )个。(2 分)
(1)量一量:$\angle ABC = ($ $ )°$,它是一个( )角。(4 分)

(2)画出表示点 $P$ 到线段 $AB$ 和 $BC$ 之间距离的线段。(4 分)
(3)在格子图中找平行四边形的第四个顶点 $D$,连接 $AD$、$CD$,画出平行四边形 $ABCD$。(2 分)
(4)在格子图中找出点 $E$,使四边形 $ABCE$ 是梯形,且上、下底的差为 $2$ cm。这样的点 $E$ 有( )个。(2 分)
答案:
(1)108 钝
(2)
过点$P$分别作$AB$和$BC$的垂线段,这两条垂线段就是点$P$到线段$AB$和$BC$之间距离的线段(图略)。
(3)
根据平行四边形对边平行且相等的性质,$AB$向右平移$3$格,再向上平移$1$格可找到点$D$(答案不唯一,只要满足平行四边形性质即可),然后连接$AD$、$CD$(图略)。
(4)2
(1)108 钝
(2)
过点$P$分别作$AB$和$BC$的垂线段,这两条垂线段就是点$P$到线段$AB$和$BC$之间距离的线段(图略)。
(3)
根据平行四边形对边平行且相等的性质,$AB$向右平移$3$格,再向上平移$1$格可找到点$D$(答案不唯一,只要满足平行四边形性质即可),然后连接$AD$、$CD$(图略)。
(4)2
1. (2025·台州路桥)如图,将一个平行四边形分成两个完全一样的直角梯形,每个直角梯形的周长是多少厘米?


答案:
1.38+20+22=80(厘米)
答:每个直角梯形的周长是80厘米。
答:每个直角梯形的周长是80厘米。
2. (2024·玉环)一个直角梯形如图,上底长 10 厘米,下底长 22 厘米。如果上底增加的长度与下底减少的长度相同,就变成了一个正方形。这个直角梯形的高是多少厘米?


答案:
2.(10+22)÷2=16(厘米)
答:这个直角梯形的高是16厘米。
答:这个直角梯形的高是16厘米。
3. (2024·绍兴上虞)有一个上底为 8 厘米、下底为 14 厘米的梯形,在这个梯形上剪一刀,刚好剪成了一个正方形和一个三角形,已知剪出的三角形中有一条边的长为 10 厘米,那么这个梯形的周长是多少? (先用铅笔在右边画出示意图,再计算)


答案:
3.
8+14+10+8=40(厘米)
答:这个梯形的周长是40厘米。
3.

8+14+10+8=40(厘米)
答:这个梯形的周长是40厘米。
查看更多完整答案,请扫码查看


