第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
20. (10分)下面是证明“三角形的外角等于与它不相邻的两个内角的和”的方法,请选择其中一种,完成证明。
已知:如图,点D是△ABC的边BC延长线上的一点。
求证:∠ACD=∠A+∠B。

已知:如图,点D是△ABC的边BC延长线上的一点。
求证:∠ACD=∠A+∠B。

答案:
20.解:
(1)
∵∠A+∠B+∠ACB=180°,
∴∠ACB=180°−(∠A+∠B)。
又∠ACB+∠ACD=180°,
∴∠ACB=180°−∠ACD。
∴180°−(∠A+∠B)=180°−∠ACD。
∴∠ACD=∠A+∠B。
(2)如图,过点C作CE//AB。
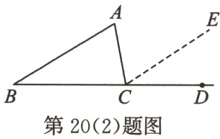
∴∠ACE=∠A,∠ECD=∠B。
∴∠ACD=∠ACE+∠ECD=∠A+∠B。
20.解:
(1)
∵∠A+∠B+∠ACB=180°,
∴∠ACB=180°−(∠A+∠B)。
又∠ACB+∠ACD=180°,
∴∠ACB=180°−∠ACD。
∴180°−(∠A+∠B)=180°−∠ACD。
∴∠ACD=∠A+∠B。
(2)如图,过点C作CE//AB。

∴∠ACE=∠A,∠ECD=∠B。
∴∠ACD=∠ACE+∠ECD=∠A+∠B。
21. (12分)
【问题发现】如图(1),在△ABC中,BE平分∠ABC,CE平分∠ACB。
(1)若∠A=70°,则∠BEC=
(2)若∠A=n°,则∠BEC=
【类比探究】
(3)如图(2),在△ABC中,BD,BE三等分∠ABC,CD,CE三等分∠ACB。若∠A=n°,则∠BEC的度数是多少?
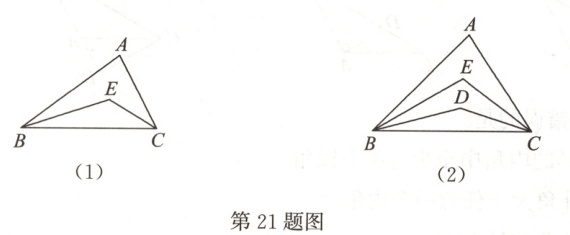
【问题发现】如图(1),在△ABC中,BE平分∠ABC,CE平分∠ACB。
(1)若∠A=70°,则∠BEC=
125°
。(2)若∠A=n°,则∠BEC=
90°+$\frac{1}{2}n°$
。【类比探究】
(3)如图(2),在△ABC中,BD,BE三等分∠ABC,CD,CE三等分∠ACB。若∠A=n°,则∠BEC的度数是多少?

答案:
21.
(1)125°
(2)90°+$\frac{1}{2}n°$
(3)解:
∵BD,BE三等分∠ABC,CD,CE三等分∠ACB,
∴∠ECB=$\frac{2}{3}$∠ACB,∠EBC=$\frac{2}{3}$∠ABC。
∴∠EBC+∠ECB=$\frac{2}{3}$(∠ABC+∠ACB)=$\frac{2}{3}$(180°−∠A)。
∴∠BEC=180°−$\frac{2}{3}$(180°−∠A)=60°+$\frac{2}{3}$∠A。
若∠A=n°,则∠BEC=(60+$\frac{2}{3}n$)°。
(1)125°
(2)90°+$\frac{1}{2}n°$
(3)解:
∵BD,BE三等分∠ABC,CD,CE三等分∠ACB,
∴∠ECB=$\frac{2}{3}$∠ACB,∠EBC=$\frac{2}{3}$∠ABC。
∴∠EBC+∠ECB=$\frac{2}{3}$(∠ABC+∠ACB)=$\frac{2}{3}$(180°−∠A)。
∴∠BEC=180°−$\frac{2}{3}$(180°−∠A)=60°+$\frac{2}{3}$∠A。
若∠A=n°,则∠BEC=(60+$\frac{2}{3}n$)°。
查看更多完整答案,请扫码查看


